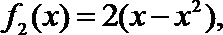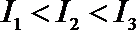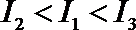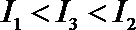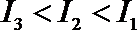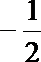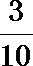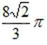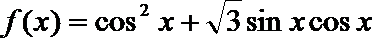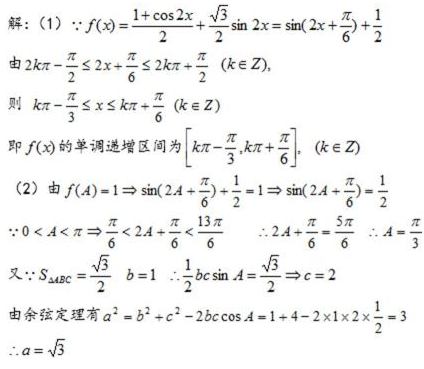- 真题试卷
- 模拟试卷
- 预测试卷
1.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 如图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知变量x,y满足约束条件

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数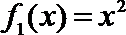
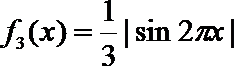
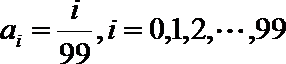
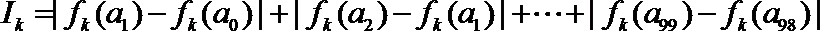
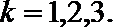
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设角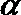
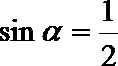
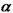
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若正数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设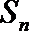
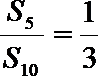
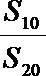
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知向量


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
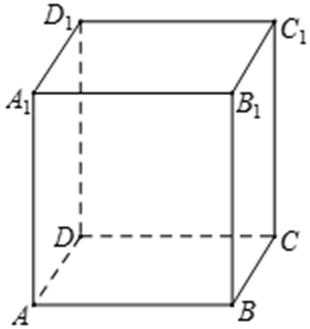
14. 如图,已知长方体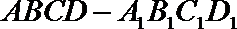
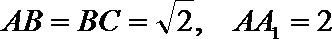

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在平面直角坐标系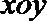

(1)求向量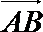
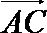
(2)若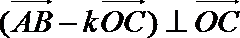
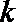
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知
(1)求
(2)设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.公差不为零的等差数列



(Ⅰ)求数列

(Ⅱ)当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(1)求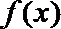
(2)在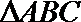



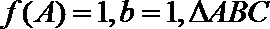
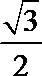

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设各项为正数的数列






(Ⅰ)求数列

(Ⅱ)设



(Ⅲ) 证明:对一切正整数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.为了提高产品的年产量,某企业拟在2014年进行技术改革,经调查测算,产品当年的产量




(1)试确定


(2)该企业2014年的技术改革费用投入多少万元时,厂家的利润最大?并求出最大利润.
正确答案
解析
解析已在路上飞奔,马上就到!