- 真题试卷
- 模拟试卷
- 预测试卷
6.已知等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 设不等式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 登山族为了了解某山高

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 执行右面的程序框图,若输出的结果为3,则可输入的实数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 在ABC中,角A、B、C所对的边长分别为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 双曲线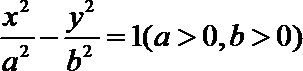
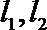
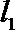
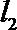
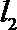
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 在三棱锥P-ABC中,侧棱PA,PB,PC两两垂直,PA=1,PB=2,PC=3,则三棱锥的外接球的表面积为______
正确答案
14
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知O为锐角ABC的外心,AB=6,AC=10,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 抛物线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 若

正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
19. 某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
(Ⅰ)根据茎叶图判断哪个区域厂家的平均分较高;
(Ⅱ)规定85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5的概率.
正确答案
(Ⅰ)东城区的平均分较高.
(Ⅱ)从两个区域各选一个优秀厂家,
则所有的基本事件共15种,
满足得分差距不超过5的事件(88,85)(88,85)(89,85)(89,94)(89,94)(93,94)(93,94)(94,,94)(94,,94)共9种.
所以满足条件的概率为
解析
解析已在路上飞奔,马上就到!
知识点
18. 如图,在三棱柱ABC-A1B1C1中,AB⊥AC,顶点


(Ⅰ)证明:平面

(Ⅱ)若点P为


正确答案
(Ⅰ)由题意得:

∴
又
∴

∵



(Ⅱ)在三棱锥

所以底面
又因为点P到底面的距离

由(Ⅰ)可知

因为点P在
所以点P到平面





所以三棱锥

解析
解析已在路上飞奔,马上就到!
知识点
20.椭圆C:
(I)求椭圆C的方程;
(II)设椭圆C的左,右顶点分别为A,B ,点P是直线
正确答案
(Ⅰ)
依题意
过焦点F与长轴垂直的直线x=c与椭圆
联立解答弦长为
所以椭圆的方程
(Ⅱ)设P(1,t)


即
可知

则
同理得到
由椭圆的对称性可知这样的定点在
不妨设这个定点为Q
又




解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数
(I)若

(II)若


正确答案
(Ⅰ)若



(Ⅱ)







即




不妨设


若





若




若




综上所述若


解析
解析已在路上飞奔,马上就到!
知识点
17. 已知
(I)求数列
(II)设数列


正确答案
(Ⅰ)设等比数列

又∵

∴
(Ⅱ)由

∴当

当



∴


两式相减得 
∴
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22〜24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.选修4-1:几何证明选讲
已知⊙O1和⊙O2相交于A,B两点,过A点作⊙O1的切线交⊙O2于点E,连接EB并延长交⊙O1于点C,直线CA交⊙O2于点D.
(Ⅰ) 当点D与点A不重合时(如图①),证明ED2=EB·EC;
(II) 当点D与点A重合时(如图②),若BC=2,BE=6,求⊙O2的直径长.
23. 选修4-4:坐标系与参数方程
在直角坐标系中,曲线C1的参数方程为:

(I)求曲线C2的直角坐标方程;
(II)若P,Q分别是曲线C1和C2上的任意一点,求|PQ|的最小值。
24. 选修4-5:不等式选讲
已知函数
(I)当

(II )若不存在实数


正确答案
22.(Ⅰ)连接AB,在EA的延长线上取点F,如图①所示.
∵AE是⊙O1的切线,切点为A,
∴∠FAC=∠ABC,.
∵∠FAC=∠DAE,
∴∠ABC=∠DAE,∵∠ABC是⊙O2内接四边形ABED的外角,
∴∠ABC=∠ADE,
∴∠DAE=∠ADE.
∴EA=ED,∵
∴
(Ⅱ)当点D与点A重合时,直线CA与⊙O2只有一个公共点,
所以直线CA与⊙O2相切.
如图②所示,由弦切角定理知:
∴AC与AE分别为⊙O1和⊙O2的直径.
∴由切割线定理知:EA2=BE·CE,而CB=2,BE=6,CE=8
∴EA2=6×8=48,AE=

23.解: (Ⅰ)
(Ⅱ)设P(



24.解:(Ⅰ)当a=1时,


当




综上可得到解集
(Ⅱ)依题意, 
则
解析
解析已在路上飞奔,马上就到!