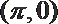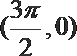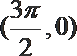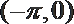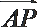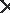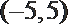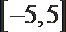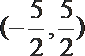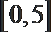- 真题试卷
- 模拟试卷
- 预测试卷
6.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.给出如下四个命题:
①若“

②“若


③“

④“

其中不正确的命题是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数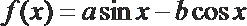
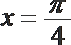
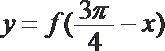
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,
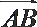
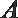
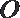
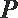
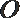
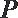
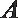
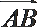
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.定义在实数集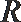
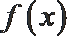
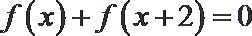
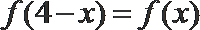
现有以下三种叙述:
①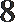
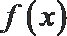
②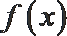
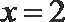
③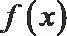
其中正确的是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在等差数列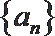
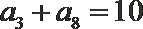
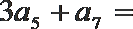
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.以下命题:
①若

②向量


③若


④若非零向量



所有真命题的序号是___________。
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
15.已知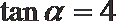
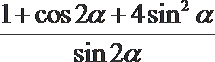
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 若将函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知函数
(Ⅰ)求函数

(Ⅱ)若对于任意的


正确答案
(Ⅰ)

∵


∴


(Ⅱ)∵对于任意的

∴


解得

解析
解析已在路上飞奔,马上就到!
知识点
20.已知




(Ⅰ)求公差
(Ⅱ)若






正确答案
(Ⅰ)∵

化简得:

(Ⅱ)由
∴ 

∴
=

又∵ 不等式



化简得:


解析
解析已在路上飞奔,马上就到!
知识点
22.选考题(请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分。)
22、已知







(Ⅰ)求证:

(Ⅱ)若

23、已知曲线





(Ⅰ)化

(Ⅱ)若








24、已知

(Ⅰ)
(Ⅱ)
正确答案
22
证:(Ⅰ)








(Ⅱ)由(1)知
又
又





23
(Ⅰ)




(Ⅱ)当










24
(Ⅰ)

(Ⅱ)





解析
解析已在路上飞奔,马上就到!
知识点
17.在



(Ⅰ)求
(Ⅱ)若


正确答案
(Ⅰ)由正弦定理可得:
所以
(Ⅱ)由余弦定理得

又



所以
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知集合



(Ⅰ)求
(Ⅱ)若

正确答案
(Ⅰ) 


(Ⅱ)
令

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(Ⅰ)讨论
(Ⅱ)若


(Ⅲ)当


正确答案
(Ⅰ) 函数


①当



②当




若



综上所述,当


当



(Ⅱ) 



令

当







(Ⅲ)当






设








当





由于


解析
解析已在路上飞奔,马上就到!