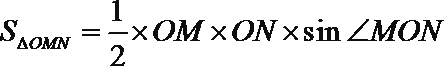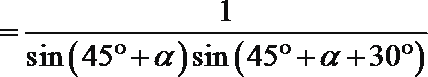- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.执行如右图所示的程序框图,则输出的
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知双曲线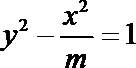
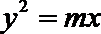
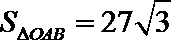
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若复数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.公差不为零的等差数列







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.某几何体的三视图如图1所示,且该几何体的体积是

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 若当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.函数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下列说法错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 若x、y满足条件

正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
15. 在正三棱锥A﹣BCD中,E,F分别是AB,BC的中点,EF⊥DE且
棱锥的四个顶点都在球O的面上,则球O的体积为__________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 数列




正确答案
1840
解析
解析已在路上飞奔,马上就到!
知识点
17. 如图,在等腰直角三角形
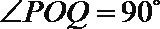

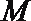
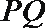
(1)若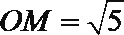
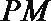
(2)若点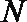
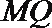
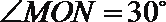
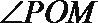
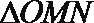
正确答案
(1)在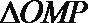
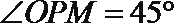
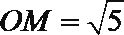
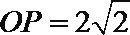
由余弦定理得,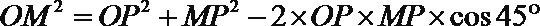
得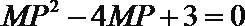


(2)设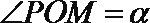
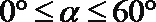
在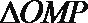
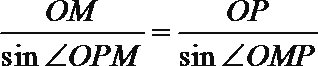
所以
故

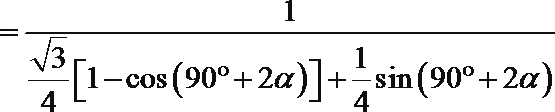
因为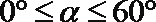
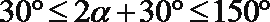
所以当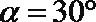
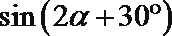
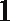
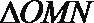
即2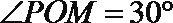
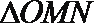
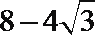
解析
解析已在路上飞奔,马上就到!
知识点
18. 如图,三角形









(Ⅰ)求证:

(Ⅱ)求几何体
正确答案
(I)
解:取


因为


所以

又因为
所以

所以




所以平面

所以

(II)取




又平面



所以

因为三角形
所以
因为


解析
解析已在路上飞奔,马上就到!
知识点
19. 为增强市民的节能环保意识,某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者,其年龄频率分布直方图如图所示,其中年龄分组区间是:
(Ⅰ)求图中

(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取5名参加中心广场的宣传活动,再从这5名中采用简单随机抽样方法选取3名志愿者担任主要负责人,求这3名志愿者中“年龄低于35岁”的人数大于1的概率。
正确答案
(I)∵小矩形的面积等于频率,
∴除
500名志愿者中,年龄在

(II)用分层抽样的方法,从中选取5名,则其中年龄“低于35岁”的人有3名,“年龄不低于35岁”的人有2名.
由列举法可得,总共为20种,
符合条件的为14种,概率为
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆


Ⅰ.求椭圆
Ⅱ.设过点







正确答案
略。
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数
(1)求
(2)如果当



正确答案
(1)定义域为
设
① 当




② 当



③ 当

令


所以



(2)

设
① 当


若

若

所以,当
② 当



综上,实数

解法二 :
设
令

所以

由洛必达法则
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第 22、 23、 24三题中任选一题做答。注意:只能做选定的题目。如果多做,则按所做的第一题计分。
22.选修 4-1:几何证明选讲
如图所示,已知








Ⅰ.求证:
Ⅱ.若


23. 选修 4-4:坐标系与参数方程
在极坐标系下,已知圆
Ⅰ.求圆

Ⅱ.当


24. 选修 4-5:不等式选讲
设函数
Ⅰ.解不等式
Ⅱ.已知关于


正确答案
22.答案:(I)证明:∵DE2=EF•EC,∠DEF公用,
∴△DEF∽△CED,∴∠EDF=∠C.又∵弦CD∥AP,∴∠P=∠C,
∴∠EDF=∠P,∠DEF=∠PEA ∴△EDF∽△EPA.
∴
∴CE•EB=EF•EP .
(II)∵DE2=EF•EC,DE=3,EF=2. ∴32=2EC,∴
∵CE:BE=3:2,∴BE=3.
由(I)可知:CE•EB=EF•EP,∴

∴BP=EP﹣EB=
∴

23.(Ⅰ)圆O:ρ=cosθ+sinθ,即ρ2=ρcosθ+ρsinθ,
所以圆O的直角坐标方程为:x2+y2=x+y,即x2+y2﹣x﹣y=0.
直线



也就是ρsinθ﹣ρcosθ=1.
则直线l的直角坐标方程为:y﹣x=1,即x﹣y+1=0.
(Ⅱ)由

故直线l与圆O公共点为(0,1),该点的一个极坐标为
24.(Ⅰ)∵f(x)=|2x+1|﹣|x﹣3|=
∴①当x<﹣
②当﹣

③当x>3时,x+4>0,∴x>3.
综上所述,不等式f(x)>0的解集为:(﹣∞,﹣4)∪(

∴当x≤﹣



当x≥3时,x+4≥7,综上所述,f(x)≥﹣
∵关于x的不等式a+3<f(x)恒成立,∴a<f(x)﹣3恒成立,
令g(x)=f(x)﹣3,则g(x)≥﹣
∴g(x)min=﹣
解析
解析已在路上飞奔,马上就到!