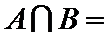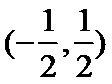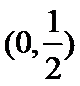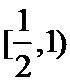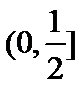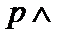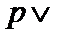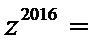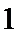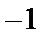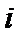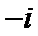- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合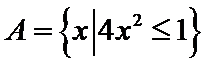
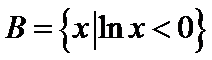
正确答案
解析
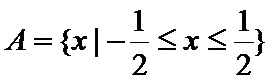
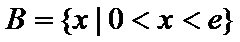
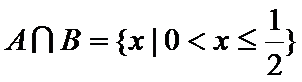
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
先解二次不等式,再解对数不等式;再借助数轴进行交集运算,即可得到结果。所以选D选项。
易错点
如何把不等号两边化为“同底”;2.解对数不等式时忽略了真数大于0。
知识点
2. 设命题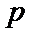
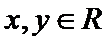
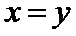
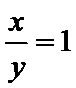
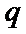
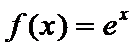
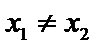
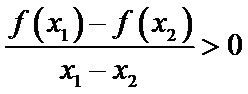
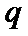
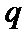
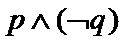
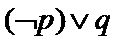

正确答案
解析
命题P中,当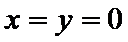
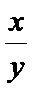
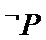
命题Q中,因为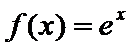
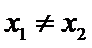
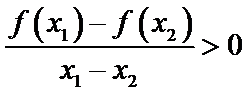
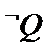
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
分别判断命题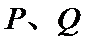
易错点
命题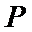

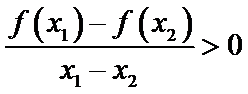
知识点
3.已知复数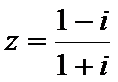
正确答案
解析
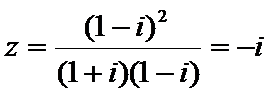
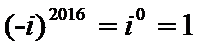
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
解题思路
先计算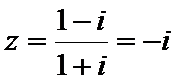
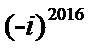
易错点
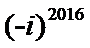
知识点
4.口袋中有四个小球,其中一个黑球三个白球,从中随机取出两个
正确答案
解析
先记“黑球”为“



符合两球同色的基本事件:


考查方向
解题思路
利用古典概率模型的解题步骤解题;用列举法列出所有的基本事件,再找到符合两球同色的基本事件个数,利用古典概率模型的概率公式
易错点
基本事件总数出错。
知识点
9.一个空间几何体的三视图如图所示,则这个几何体的表面积为
正确答案
解析
由三视图得,几何体为棱长都为
因为三棱锥的四个面全等,所以三棱锥的表面积
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
由三视图得几何体为多面体;多面体的表面积为各个面面积之和。
易错点
由三视图推导不出原几何体的形状。
知识点
10. 已知数列




正确答案
解析
由










A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
由等差数列等比数列的性质,把

作差法比较大小。
易错点
等差等比数列性质不熟悉,没有发现第


转化思想,没想到把

知识点
5.已知



正确答案
解析
约束条件对应的可行域如图
把目标函数化为直线的斜截式


将点


A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
准确画出约束条件对应的可行域;找到最优解;把最优解代入目标函数,求出目标函数的最值。
易错点
可行域画错;求目标函数的最大值即找截距的最小值,错认为求截距的最大值。
知识点
6.已知函数



正确答案
解析
把图象上的点







B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
解题思路
代入法。把图象上的点代入,求出

易错点
易错选为C。
知识点
7.在平面直角坐标系中,双曲线




正确答案
解析
已知双曲线的渐近线方程为

把点



A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
已知双曲线的渐近线方程

把所给点代入上面方程,即得
易错点
双曲线的焦点位置不好确定,不会设双曲线方程的形式。
知识点
8.如图,给出的是求

程序框图,则判断框内填入的条件是
正确答案
解析
当



以此类推,当




A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
找到求和规律;
找到终止循环的条件。
易错点
没看清“是”,“否”,不等号方向写反,本题循环结构为
当型循环,当满足条件时执行循环体,因此排除A,D项;求和后,




知识点
11.等腰直角










所在圆的半径)
正确答案
解析
因为圆




当圆



A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
由圆心




易错点
易错选为A。
知识点
12.已知函数


正确答案
解析







①当







②当



当







当










综合①②知,
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
先写出


分




易错点
不会画含参数的二次函数图象;
不会用导函数研究原函数的图象,当所给函数不是基本初等函数时,我们可通过求导来研究原函数的图象。
知识点







正确答案
解析

设



考查方向
解题思路
根据三点共线定理,得到





易错点
三点共线定理的运用;根据

知识点
13.已知圆
正确答案
解析
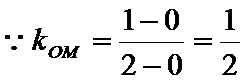
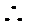

考查方向
解题思路
易错点
没发现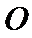
知识点
14.数列




正确答案
解析
当

故
考查方向
解题思路
将递推公式转化成


易错点
忘了同底指数幂相乘的运算法则;2.指数位置应是

知识点
16.四棱锥




正确答案
解析
可求得正方形









考查方向
解题思路
求出球心到正方形的中心的距离,再结合图形判断位置关系求解.
易错点
球心位置的确定
知识点
棱长为1的正方体





21.当


22.当平面



正确答案
(Ⅰ)略;
解析
(Ⅰ)连接


正方体









考查方向
线面、面面垂直的判定与性质,棱柱、棱锥体积的求法.
解题思路
证



易错点
通过证线面垂直得线线垂直;判断
正确答案

解析
当

取






















设



考查方向
解题思路
证



易错点
通过证线面垂直得线线垂直;判断
已知
17.若







正确答案
解析
(Ⅰ)



考查方向
解题思路
化简


易错点
通过降幂公式、辅助角公式化简

正确答案

解析









考查方向
解题思路
化简


易错点
通过降幂公式、辅助角公式化简

某汽车公司为了考查某4S店的服务态度,对到店维修保养的客户进行回访调查,每个用户在到此店维修或保养后可以对该店进行打分,最高分为10分.上个月公司对该4S店的100位到店维修保养的客户进行了调查,将打分的客户按所打分值分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到频率分布直方图如图所示.
19.分别求第四、五组的频率;
20.该公司在第二、三组客户中按分层抽样的方法抽取6名客户进行深入调查,之
后将从这6人中随机抽取2人进行物质奖励,求得到奖励的人来自不同组的概率.
正确答案
第四、五组的频率分别为
解析
由直方图知,第四组的频率为



考查方向
解题思路
求出四、五组的矩形面积即为频率;列举法求解古典概型.
易错点
频率分布直方图的纵轴表示的是频率/組距;古典概型的解题步骤规范性.
正确答案

解析
(1)由直方图知,第四组的频率为



(2) 由直方图知,第二、三组客户人数分别为10人和20人,所以抽出的6人中,第二组有2人,设为A,B,第三组有4人,设为a,b,c,d.
从中随机抽取2人的所有情况如下:
AB,Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,ab,ac,ad,bc,bd,cd共15种.…8分
其中,两人来自不同组的情况共有8种, 分别是Aa,Ab,Ac,Ad,Ba,Bb,Bc,Bd,…10分
所以,得到奖励的人来自不同组的概率为
考查方向
解题思路
求出四、五组的矩形面积即为频率;列举法求解古典概型.
易错点
频率分布直方图的纵轴表示的是频率/組距;古典概型的解题步骤规范性.
已知抛物线


23.求抛物线C的方程;
24.已知动圆P的圆心在抛物线C上,且过定点D(0,4),若动圆P与x轴交于A、B两点,且

正确答案
(Ⅰ)
解析
(1) 设抛物线的焦点为

由








考查方向
解题思路
过抛物线焦点的弦长运用抛物线的定义可求得;求出
易错点
本题抛物线为开口向上的,故焦点弦长为

正确答案

解析
设动圆圆心

且圆
令

解得:

当

当




所以

考查方向
解题思路
过抛物线焦点的弦长运用抛物线的定义可求得;求出
易错点
本题抛物线为开口向上的,故焦点弦长为

已知函数



25.求函数
26.求证:
正确答案
(Ⅰ)

解析
解:(1)
令



令



考查方向
解题思路
在(Ⅱ)中要构造函数,通过求导研究单调性.
易错点
求单调性注意定义域;导数的运算.
正确答案
(Ⅱ)略.
解析


则
令
则


而



即

则





则


故

故
考查方向
解题思路
在(Ⅱ)中要构造函数,通过求导研究单调性.
易错点
求单调性注意定义域;导数的运算.
等腰梯形











27.求证:
28.若



正确答案
略;
解析
(1) 




考查方向
解题思路
根据切割线定理得



易错点
难以找出相等的角,进而将边转化求长度.
正确答案

解析




考查方向
解题思路
根据切割线定理得



易错点
难以找出相等的角,进而将边转化求长度.