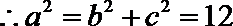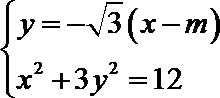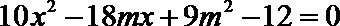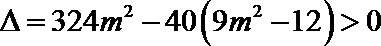- 真题试卷
- 模拟试卷
- 预测试卷
1.对于集合





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.侧面展开图是半径长为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.不等式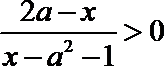
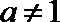
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.用系统抽样法要从










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若复数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若变量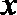
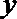
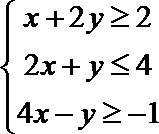
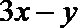
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.从个位数与十位数之和为奇数的两位数中任取一个,其十位数比个位数大的概率是( ).
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知二次不等式



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设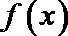
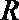
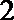
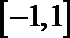
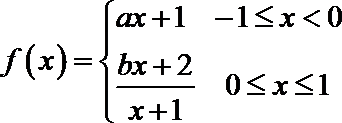
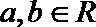

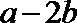
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.二项式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.一个水平放置的三角形的斜二测直观图是一个斜边水平,腰长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设

①
②
③
④
则其中可作为使
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知


(1)求数列
(2)记






正确答案
(1)由


代入
(2)
化简可得:


解析
解析已在路上飞奔,马上就到!
知识点
22.定义非零向量






(1)已知

(2)求(1)中函数
(3)已知点







正确答案
(1)



(2)


(3)

其中
当




令
当
解析
解析已在路上飞奔,马上就到!
知识点
20.在直三棱柱








(1)画出此三棱柱的左视图和俯视图;
(2)求三棱锥
正确答案
(1)左视图为正方形
俯视图为直角三角形
(2)








可得:
解析
解析已在路上飞奔,马上就到!
知识点
21.已知圆
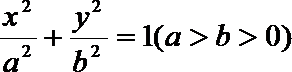
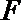

(1)求椭圆的方程;
(2)过椭圆外一点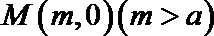

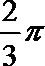
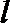
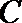
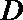
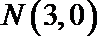
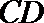
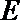
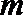
正确答案
(1)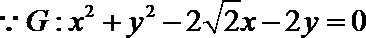
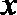
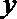
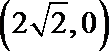
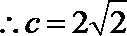

(2)设直线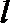
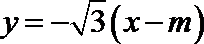
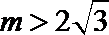
可得:
可得:
即
设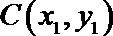

则
化简得:
可得: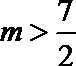
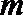
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数



(1)求
(2)问:是否存在边长为







(3)若函数




正确答案
(1)把

可得:
化简此方程组可得:
即
可得

代入原方程组可得:
(2)由

此三角形的高即点






即





直线
即
(3)由题意知:












又


解析
解析已在路上飞奔,马上就到!