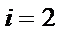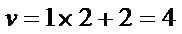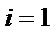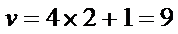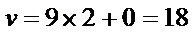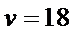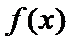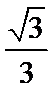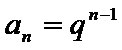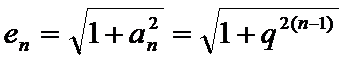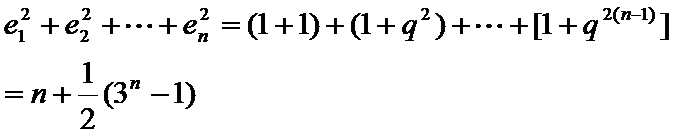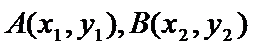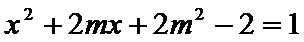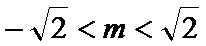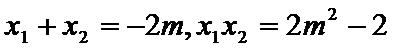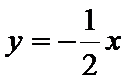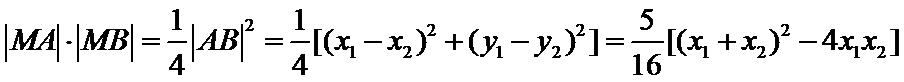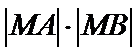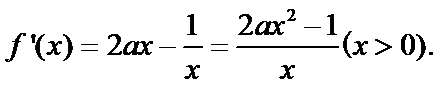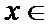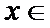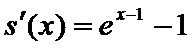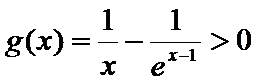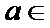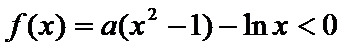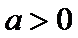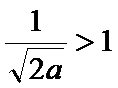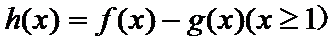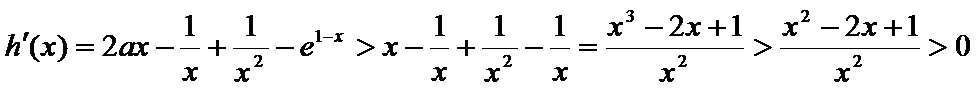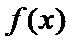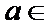- 真题试卷
- 模拟试卷
- 预测试卷
1.设i为虚数单位,则复数(1+i)2=( )
正确答案
解析
考查方向
解题思路
本题考查复数的乘法运算,具体解题步骤如下:1.进行复数的乘法运算。2.整理为a+bi形式
易错点
本题易在复数相等时错误,等式左右两边都写成a+bi形式,导致题目出现错误。
知识点
3.抛物线y2=4x的焦点坐标是( )
正确答案
解析
抛物线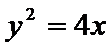
考查方向
解题思路
本题考查抛物线的几何性质,具体解题步骤如下:直接求出抛物线的准线方程
易错点
本题易在记忆抛物线的焦点坐标出错。
知识点
5.设p:实数x.y满足x>1且y>1,q: 实数x,y满足x+y>2,则p是q的( )
正确答案
解析
由题意,







考查方向
解题思路
本题先看p与q的关系,再看q与p的关系.
易错点
本题容易把条件、结论弄混;必要条件判断易错。
知识点
7.某公司为激励创新,计划逐年加大研发奖金投入。若该公司2015年全年投入研发奖金130万元,在此基础上,每年投入的研发奖金比上一年增长12%,则该公司全年投入的研发奖金开始超过200万元的年份是(参考数据:lg1.12=0.05,lg1.3=0.11,lg2=0.30) ( )
正确答案
解析
试题分析:设从2015年后第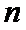
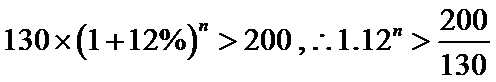
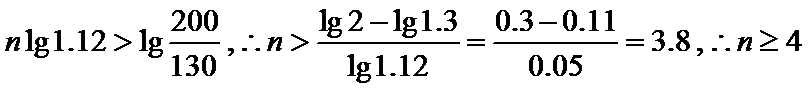
考查方向
解题思路
本题先根据题意得出不等式,然后两边同取对数,可以得到n的范围,求出奖金开始超过200万元的年份.
易错点
本题在解不等式的时候想不到两边取对数的技巧
知识点
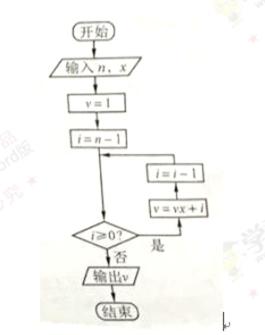
8.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法。如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为( )
正确答案
解析
初始值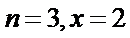
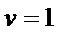
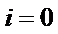
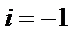
考查方向
解题思路
本题考查程序框图,具体解题步骤是把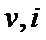
循环结构,基本方法是将每次循环的结果一一列举
易错点
本题易在写过程时发生错误。
知识点
2.设集合A={x|1≤x≤5},Z为整数集,则集合A∩Z中元素的个数是( )
正确答案
解析
由题意可知
考查方向
解题思路
本题可以对两个集合取交集就可以得出结果.
易错点
本题主要考查的是集合的交集属于容易题.注意Z为整数集,否则很容易出现错误.
知识点
4.为了得到函数y=sin
正确答案
解析
由题意,为得到函数


考查方向
解题思路
本题y=sin x 是平移前的曲线,向左平移

易错点
本题容易把平移前和平移后的曲线弄混.
知识点
6.已知a函数f(x)=x3-12x的极小值点,则a=( )
正确答案
解析
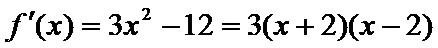
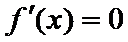
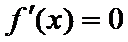
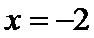
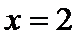
在(-2,2)上单调递减,在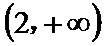
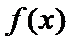
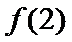
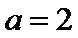
考查方向
解题思路
本题可以先求出函数的导数,然后解不等式得出函数的单调性,从而得出极值。
易错点
本题在求导判断极值点时易错。
知识点
9.已知正三角形ABC的边长为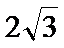
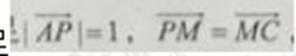
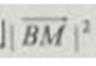
正确答案
解析
所以正三角形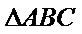
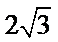
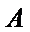
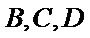
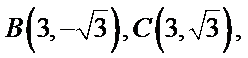
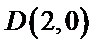
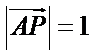
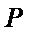
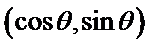
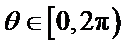
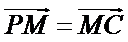
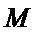
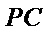
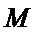
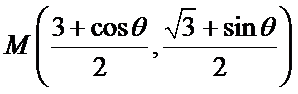
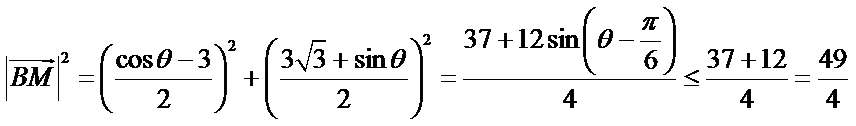
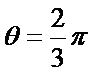
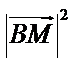
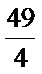
考查方向
解题思路
本题考查平面向量的数量积与向量的模,由于结论是要求向量模的平方的最大值,因此我们要把它用一个参数表示出来,解题时首先对条件进行化简变形,本题中得出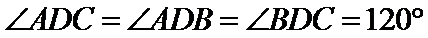
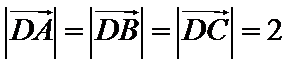
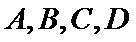

易错点
本题易在几何意义中发生错误.
知识点
10.设直线l1,l2分别是函数f(x)= 
正确答案
解析
设














考查方向
解题思路
本题首先考查导数的几何意义,其次考查最值问题,解题时可设出切点坐标,利用切线垂直求出这两点的关系,同时得出切线方程,从而得点


易错点
本题考查导数的几何意义,其次考查最值问题,解题时可设出切点坐标,在求切线方程的时候易错。
知识点
11.sin750°= 。
正确答案
解析
由诱导公式可得
考查方向
解题思路
本题也可以看作是一个来自于课本的题,直接利用课本公式解题,这告诉我们一定要立足于课本.有许多
易错点
本题考查了三角函数诱导公式的问题,在诱导公式的应用中易错。
知识点
13.从2、3、8、9任取两个不同的数值,分别记为a、b,则
正确答案
解析
从2,3,8,9中任取两个数为



考查方向
解题思路
本题考查古典概型,解题关键是求出基本事件的总数,本题中所给数都可以作为对数的底面,因此所有对数的个数就相当于4个数中任取两个的全排列,个数为
易错点
本题考查古典概型,解题关键是求出基本事件的总数,和事件A发生的事件数易错。
知识点
12.已知某三菱锥的三视图如图所示,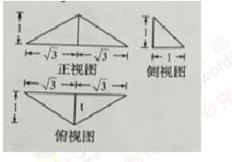
正确答案
解析
由三视图可知该几何体是一个三棱锥,且底面积为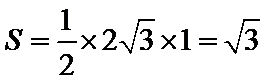
考查方向
解题思路
本题考查三视图,考查几何体体积,考查学生的识图能力.解题时要求我们根据三视图想象出几何体的形状,由三视图得出几何体的尺寸,为此我们必须掌握基本几何体(柱、锥、台、球)的三视图以及各种组合体的三视图.
易错点
本题易在观察三视图的量的时候出错。
知识点
14.若函数f(x)是定义R上的周期为2的奇函数,当0

正确答案
-2
解析
首先,





又



考查方向
解题思路
本题考查函数的奇偶性与周期性.属于基础题,在涉及函数求值问题中,可利用周期性
易错点
本题考查函数的奇偶性与周期性.属于基础题,在涉及函数求值问题中,在涉及到奇偶性时易出错。
知识点
15.在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为P(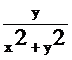
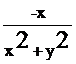
①若点A的“伴随点”是点A′,则点A′的“伴随点”是点A.
②单位圆上的点的“伴随点”仍在单位圆上;
③若两点关于x轴对称,则它们的“伴随点”关于y轴对称;
④若三点在同一条直线上,则它们的“伴随点”一定共线.
其中的真命题是 (写出所有真命题的序号).
正确答案
②③
解析
① 设
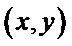
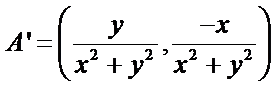
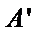
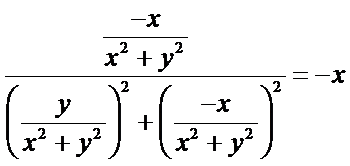
故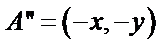
② 设单位圆上的点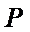
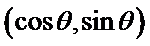
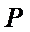
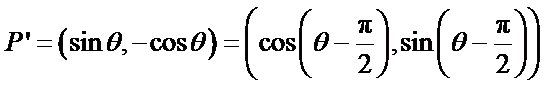
所以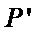
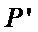
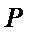
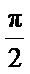
③ 设曲线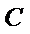
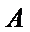
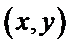
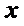
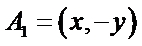
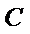
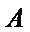
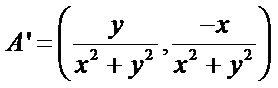
点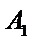
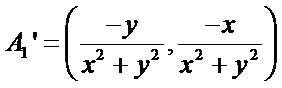
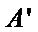
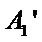
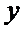
④ 反例:例如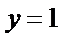
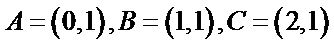
随点分别是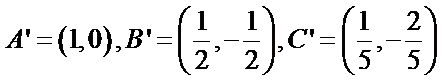
设点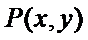
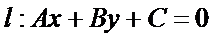

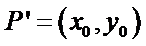
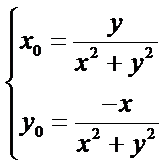
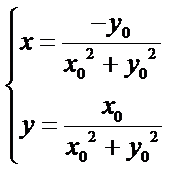
带入直线方程可知: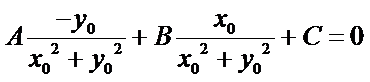
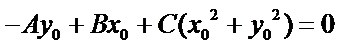
当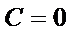
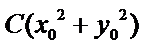
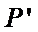
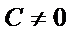
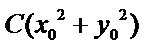
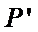
所以,直线“伴随曲线”不一定是一条直线. 错误.
考查方向
解题思路
本题考查了新定义问题与曲线与方程的问题.
易错点
本题考查新定义问题,属于创新题,符合新高考的走向.它考查学生的阅读理解能力,接受新思维的能力。本题容易在理解定义时出错。
知识点
已知数列{an}的首项为1, Sn为数列{an}的前n项和,Sn+1=qSn+1,其中q﹥0,n∈N+
23.若a2,a3,a2+a3成等差数列,求数列{an}的通项公式;
24.设双曲线x2﹣=1的离心率为en,且e2=2,求e12+ e22+…+en2,
正确答案
(Ⅰ)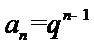
解析
(Ⅰ)由已知,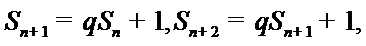

又由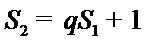
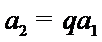
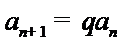
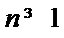
所以,数列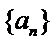
从而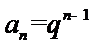
由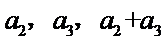
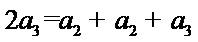
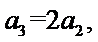
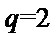
所以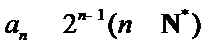
考查方向
解题思路
先利用双曲线的离心率定义得到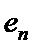
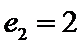
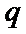
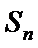
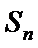
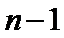
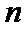
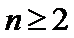
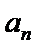

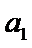
易错点
本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识,在求离心率时易错。
正确答案
(Ⅱ)
解析
(Ⅱ)由题意可得,
所以双曲线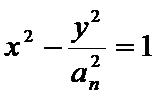
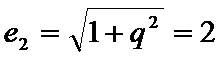
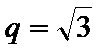
考查方向
解题思路
先利用双曲线的离心率定义得到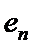
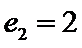
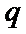
易错点
本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识,在求离心率时易错。
已知椭圆E:+=1(a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点P(,)在椭圆E上。
25.求椭圆E的方程;
26.设不过原点O且斜率为的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:︳MA︳·︳MB︳=︳MC︳·︳MD︳
正确答案
(1)
解析
(I)由已知,a=2b.
又椭圆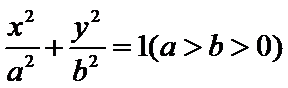
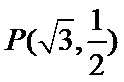
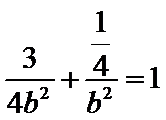
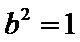
所以椭圆E的方程是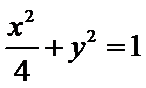
考查方向
解题思路
由椭圆两个焦点与短轴的一个端点是正三角形的三个顶点可得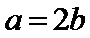
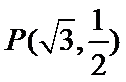
易错点
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆(圆锥曲线)的交点问题,联立化简易出错。
正确答案
(Ⅱ)设直线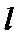
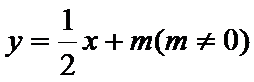
由方程组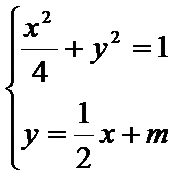
判别式为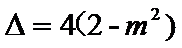
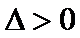
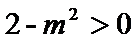
由根与系数的关系可得
所以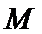
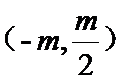
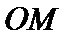
联立可得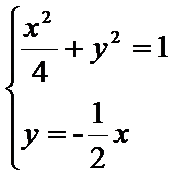
所以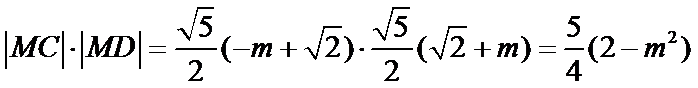
又
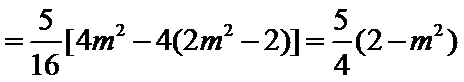
所以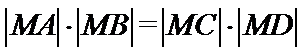
解析
(Ⅱ)设直线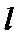
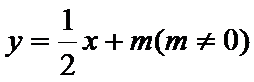
由方程组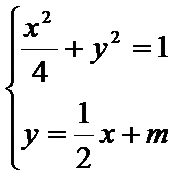
判别式为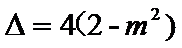
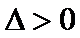
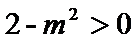
由根与系数的关系可得
所以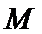
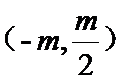
联立可得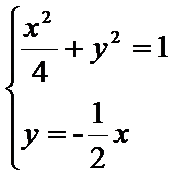
所以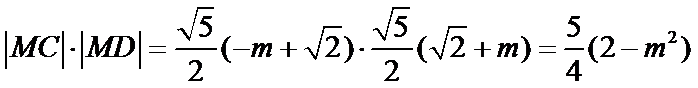
又
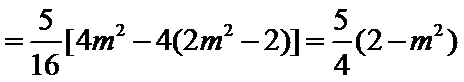
所以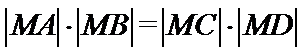
考查方向
解题思路
(Ⅱ)首先设出直线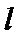
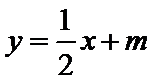
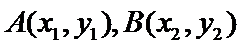
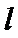

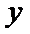
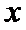
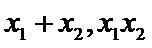
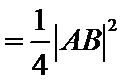
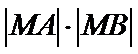
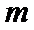
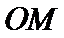
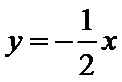
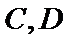
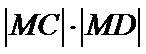
易错点
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆(圆锥曲线)的交点问题,联立化简易出错。
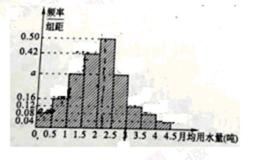
我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5), [0.5,1),……[4,4.5]分成9组,制成了如图所示的频率分布直方图。
16.求直方图中的a值;
17.设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
18.估计居民月均用水量的中位数.
正确答案
(Ⅰ)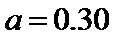
解析
(Ⅰ)由频率分布直方图,可知:月用水量在[0,0.5]的频率为0.08×0.5=0.04
同理,在[0.5,1),(1.5,2],[2,2.5),[3,3.5),[3.5,4),[4,4.5)等组的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.
由1–(0.04+0.08+0.21+.025+0.06+0.04+0.02)=0.5×a+0.5×a,
解得a=0.30.
考查方向
解题思路
本题主要考查频率分布直方图、频率、频数的计算公式等基础知识,考查学生的分析问题解决问题的能力.在频率分布直方图中,第个小矩形面积就是相应的频率或概率,所有小矩形面积之和为1,这是解题的关键,也是识图的基础.
易错点
本题主要考查频率分布直方图、频率、频数的计算公式等基础知识,易在计算中出错。
正确答案
(Ⅱ)36000;
解析
(Ⅱ)由(Ⅰ),100位居民月均水量不低于3吨的频率为0.06+0.04+0.02=0.12.
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为300000×0.13=36000.
考查方向
解题思路
本题主要考查频率分布直方图、频率、频数的计算公式等基础知识,考查学生的分析问题解决问题的能力.在频率分布直方图中,第个小矩形面积就是相应的频率或概率,所有小矩形面积之和为1,这是解题的关键,也是识图的基础.
易错点
本题主要考查频率分布直方图、频率、频数的计算公式等基础知识,易在计算中出错。
正确答案
(Ⅲ)2.04.
解析
(Ⅲ)设中位数为x吨.
因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,
而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5
所以2≤x<2.5.
由0.50×(x–2)=0.5–0.48,解得x=2.04.
故可估计居民月均用水量的中位数为2.04吨.
考查方向
解题思路
本题主要考查频率分布直方图、频率、频数的计算公式等基础知识,考查学生的分析问题解决问题的能力.在频率分布直方图中,第个小矩形面积就是相应的频率或概率,所有小矩形面积之和为1,这是解题的关键,也是识图的基础.
易错点
本题主要考查频率分布直方图、频率、频数的计算公式等基础知识,易在计算中出错。
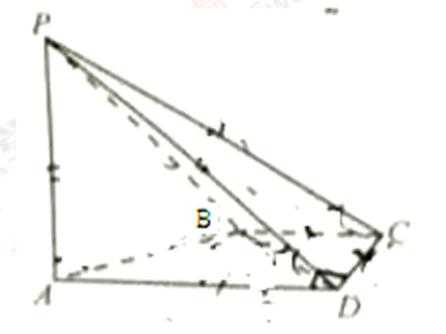
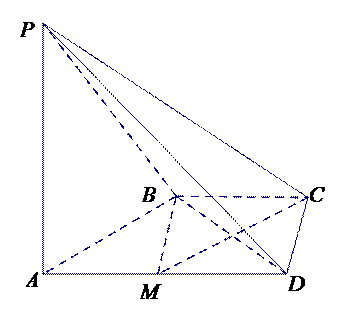
如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,BC=CD=½AD。
19.在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由;
20.证明:平面PAB⊥平面PBD。
正确答案
(Ⅰ)取棱AD的中点M,证明详见解析;
解析
(I)取棱AD的中点M(M∈平面PAD),点M即为所求的一个点.理由如下:
因为AD‖BC,BC=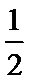
所以四边形AMCB是平行四边形,从而CM‖AB.
又AB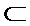
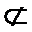
所以CM∥平面PAB.
(说明:取棱PD的中点N,则所找的点可以是直线MN上任意一点)
考查方向
解题思路
本题考查线面平行、面面垂直的判断,考查空间想象能力、分析问题的能力、计算能力.证明线面平行时,可根据判定定理的条件在平面内找一条平行线,而这条平行线一般是由过面外的直线的一个平面与此平面相交而得,证明时注意定理的另外两个条件(线在面内,线在面外)要写全,否则会被扣分,求线面角(以及其他角),证明面面垂直时,要证线面垂直,要善于从图形中观察有哪些线线垂直,从而可能有哪个线面垂直,确定要证哪个线线垂直,切忌不加思考,随便写.
易错点
本题考查线面平行、面面垂直的判断,考查空间想象能力、分析问题的能力、计算能力.证明线面平行时,容易在证明平行时步骤不全面出现错误。
正确答案
(II)由已知,PA⊥AB, PA ⊥ CD,
因为AD∥BC,BC=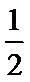
所以PA ⊥平面ABCD.
从而PA ⊥ BD.
因为AD∥BC,BC=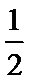
所以BC∥MD,且BC=MD.
所以四边形BCDM是平行四边形.
所以BM=CD=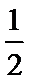
又AB∩AP=A,所以BD⊥平面PAB.
又BD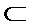
所以平面PAB⊥平面PBD.
解析
(II)由已知,PA⊥AB, PA ⊥ CD,
因为AD∥BC,BC=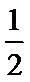
所以PA ⊥平面ABCD.
从而PA ⊥ BD.
因为AD∥BC,BC=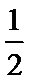
所以BC∥MD,且BC=MD.
所以四边形BCDM是平行四边形.
所以BM=CD=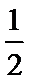
又AB∩AP=A,所以BD⊥平面PAB.
又BD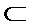
所以平面PAB⊥平面PBD.
考查方向
解题思路
本题考查线面平行、面面垂直的判断,考查空间想象能力、分析问题的能力、计算能力.证明线面平行时,可根据判定定理的条件在平面内找一条平行线,而这条平行线一般是由过面外的直线的一个平面与此平面相交而得,证明时注意定理的另外两个条件(线在面内,线在面外)要写全,否则会被扣分,求线面角(以及其他角),证明面面垂直时,要证线面垂直,要善于从图形中观察有哪些线线垂直,从而可能有哪个线面垂直,确定要证哪个线线垂直,切忌不加思考,随便写.
易错点
本题考查线面平行、面面垂直的判断,考查空间想象能力、分析问题的能力、计算能力.证明线面平行时,容易在证明平行时步骤不全面出现错误。
在△ABC中,角A,B,C所对的边分别是a,b,c,且
21.证明:sinAsinB=sinC;
22.若
正确答案
(Ⅰ)根据正弦定理,可设


则a=ksin A,b=ksin B,c=ksin C.
代入





sin Asin B=sin Acos B+cos Asin B=sin(A+B).
在△ABC中,由A+B+C=π,有sin(A+B)=sin(π–C)=sin
所以sin Asin B
解析
(Ⅰ)根据正弦定理,可设


则a=ksin A,b=ksin B,c=ksin C.
代入





sin Asin B=sin Acos B+cos Asin B=sin(A+B).
在△ABC中,由A+B+C=π,有sin(A+B)=sin(π–C)=sin
所以sin Asin B
考查方向
解题思路
本题考查正弦定理、余弦定理、商数关系等基础知识,考查学生的分析问题的能力和计算能力.在解三角形的应用中,凡是遇到等式中有边又有角时,可用正弦定理进行边角互化,一种是化为三角函数问题,一般是化为代数式变形问题.在角的变化过程中注意三角形的内角和为
易错点
本题考查正弦定理、余弦定理、商数关系等基础知识,考查学生的分析问题的能力,在化边为角和化角为边时易错。
正确答案
(Ⅱ)4.
解析
(Ⅱ)由已知,b2+c2–a2=
cos A=

所以sin A=

由(Ⅰ),sin Asin B=sin Acos B+cos Asin B,
所以


故
考查方向
解题思路
本题考查正弦定理、余弦定理、商数关系等基础知识,考查学生的分析问题的能力和计算能力.在解三角形的应用中,凡是遇到等式中有边又有角时,可用正弦定理进行边角互化,一种是化为三角函数问题,一般是化为代数式变形问题.在角的变化过程中注意三角形的内角和为
易错点
本题考查正弦定理、余弦定理、商数关系等基础知识,考查学生的分析问题的能力,在化边为角和化角为边时易错。
设函数f(x)=ax2-a-lnx,g(x)=-,其中a∈R,e=2.718…为自然对数的底数。
27.讨论f(x)的单调性;
28.证明:当x>1时,g(x)>0;
29.确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立。
正确答案
(1)当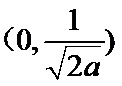
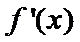
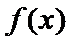
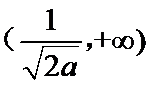
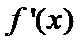
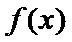
解析
(I)
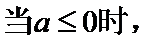
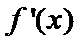
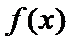
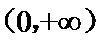
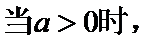
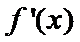
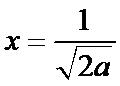
当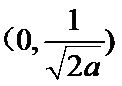
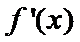
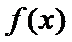
当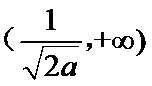
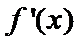
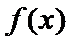
考查方向
解题思路
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,考查学生的分析问题解决问题的能力和计算能力.求函数的单调性,基本方法是求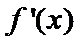
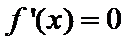
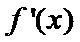
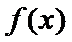
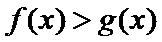
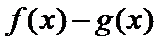
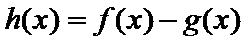
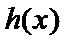
易错点
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,易在构造函数时发生错误。
正确答案
(Ⅱ)证明:令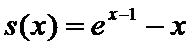
当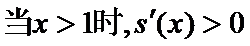
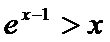
解析
(Ⅱ)证明:令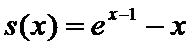
当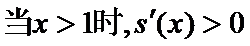
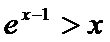
考查方向
解题思路
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,考查学生的分析问题解决问题的能力和计算能力.求函数的单调性,基本方法是求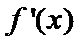
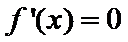
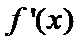
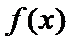
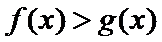
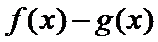
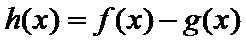
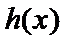
易错点
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,易在构造函数时发生错误。
正确答案
(3)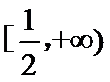
解析
(Ⅲ)由(Ⅱ)可得,当x>1时,g(x)>0;
当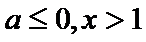
故当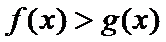
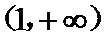
当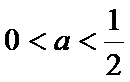
由(Ⅰ)得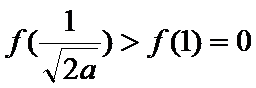
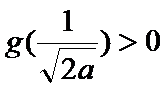
所以此时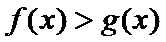
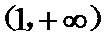
当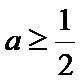
当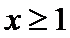
因此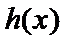
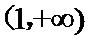
又因为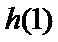
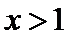
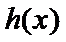
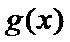
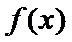
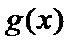
综上,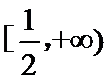
考查方向
解题思路
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,考查学生的分析问题解决问题的能力和计算能力.求函数的单调性,基本方法是求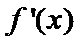
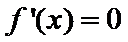
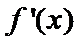
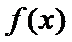
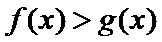
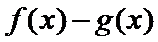
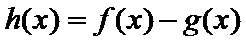
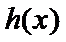
易错点
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,易在构造函数时发生错误。