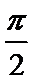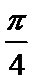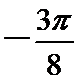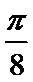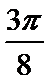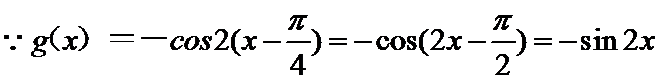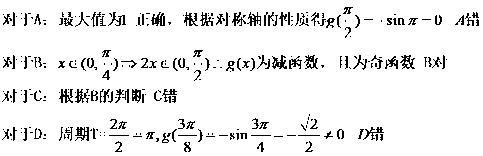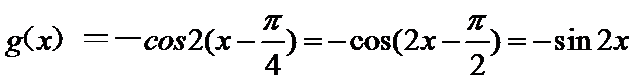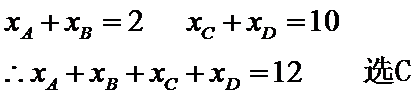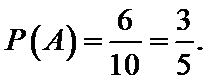- 真题试卷
- 模拟试卷
- 预测试卷
2.命题“

正确答案
解析
根据全(特)称命题的否定:存在性命题的否定是全称命题,排除CD,再根据语句要否定,排除B,选择A
考查方向
解题思路
根据存在性命题的否定直接得出结果
易错点
本题易错于全(特)称命题的否定的形式,导致无法排除
知识点
4.设θ为第四象限的角,cosθ=
正确答案
解析
由题意可知

考查方向
解题思路
1)利用余弦值求正弦值,注意象限,
2)利用正弦的倍角公式,直接计算结果
易错点
本题易于象限对应的三角函数值的正负判断出错
知识点
6.经过点(2,1),且渐近线与圆
正确答案
解析
设渐近线方程为
∴渐近线为
∴设双曲线方程为
考查方向
解题思路
1)设渐近线方程
2)利用渐近线写出含参双曲线方程,带入坐标直接得出结果
易错点
本题易在双曲线焦点的判断
知识点
8.将函数f(x)=-cos2x的图象向右
正确答案
解析
所以可以判断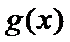
考查方向
解题思路
1)根据平移变换和诱导公式得到
2)根据三角函数的图像的性质对选项一一验证得出选项
易错点
主要易错于平移变换出错
知识点
3.定义运算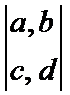
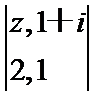
正确答案
解析
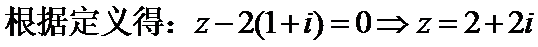
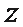
考查方向
解题思路
本题属于简单题,可使用直接法,
(1)化简z得到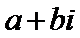
(2)观察实部和虚部对应的正负
易错点
计算过程忽视定义的规律出错
知识点
1.已知集合A={x|x≥4},B={x|-1≤2x-1≤0},则CRA∩B=
正确答案
解析
考查方向
解题思路
本题属于简单题,可使用数轴表示出集合直接判断,
易错点
该题主要易错于对端点情况的判断错误
知识点
9.如图是正三棱锥V-ABC的正视图、侧视图和俯视图,则其侧视图的面积是
正确答案
解析
如图计算底面高
体高
所以侧面积
考查方向
解题思路
1)根据三视图得出底边长为
2)计算体高VA,得出结果
易错点
主要易错于读错数据
知识点
10.已知定义在R上的奇函数y=f(x)
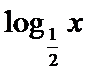
正确答案
解析
根据性质做出图像
共有4个零点ABCD,且AB关于x=1对称
CD关于x=5对称
考查方向
解题思路
1)根据函数性质得出函数在(0,6)上的图像,
2)数形结合得到零点
3)根据对称性得出零点间关系
易错点
主要易错于函数图像不能有效的画出
知识点
5.某程序框图如图所示,则该程序运行后输出的值是
正确答案
解析
不难发现有周期性变化,周期为4,所以
考查方向
解题思路
1)写出循环结构,找出S结果的规律
2)根据周期性找出周期
3)找出跳出循环的位置
易错点
本题易在判断上出错,导致提前或者延后跳出循环,第二没有发现S结果之间的规律,导致出错,
知识点
7.平面内满足约束条件



正确答案
解析
画出可行域
由图可知平移2x+y=0,得到最小距离时经过点A(1,1),因为过点A的直线方程为2x+y-3=0,根据平行线之间的距离可得
考查方向
解题思路
1)画出可行域,标记2x+y=0
2)找到可行域到2x+y=0的最短距离,做平行线求最优解
3)根据对称性可知所求答案即最短距离的2倍
易错点
主要体现在①可行域不规范,②直线平移过程忽略直线的斜率,③题意理解错误
知识点
11.设数列{



是
正确答案
解析
构造新数列{


∴{
∴
考查方向
解题思路
1)根据数列递推关系,构造新数列{

2)得出新数列为等差数列,求出
3)还原得到a20
易错点
主要易错于无法构造新数列,导致解题步骤加长,计算出错
知识点
12.对

正确答案
解析
考查方向
解题思路
1)由向量可知
2)向量转化问题变为圆的方程
长度不超过6等价于
3)问题转化为两圆内切或内涵,进而求出n的范围
4)根据几何概型得出结果
易错点
主要易错于几何意义的构建
知识点
15.已知正数x,y满足
正确答案
3
解析
考查方向
解题思路
1)令2x+y=t→y=t-2x带入计算
2)化简可以得到
易错点
主要易错于均值定理的构建过程
知识点
16.在正三棱锥V—ABC内,有一半球,其底面与正三棱锥的底面重合,且与正三棱锥的三个侧面都相切,若半球的半径为2,
正确答案
解析
设球心为O,设底边OD=x和体高OP=x,如图:则
考查方向
解题思路
1)设底边长a和侧高l
2)把三棱锥的体积分割成以球心为定点的三个三棱锥,求体积之和即椎体的体积
3)根据体积求出a.l的关系
4)利用公式计算体高
易错点
主要易错于球的几何性质用错
知识点
13.曲线f(x)=
正确答案
解析
考查方向
解题思路
1)对曲线函数求导,
2)求点P出的导函数值即斜率
3)使用点斜式直接写出答案
易错点
主要易错于求导出错
知识点
14.已知{

正确答案
-1
解析
考查方向
解题思路
1)使用等差数列通项公式使用a1和d表示
2)使用等比中项公式得到关系式
易错点
主要易错于计算出错
知识点
在△ABC中,角A、B、C所对的边分别为a、b、c,且满足cos2C-cos2A=2sin(

17.求角A的值;
18.若a=
正确答案
见解析
解析
解:(1)由已知得
化简得

考查方向
解题思路
该题解题思路如下
1)利用倍角公式
2)利用特殊角的三角函数求值得到角A,
3)使用正弦定理,进行边角之间的转换
4)根据角的取值范围得到答案
易错点
该题易于忽略了对A的范围的判断,该题属于中档题
正确答案
见解析
解析
解:
(2)由正弦定理

因为


故
所以
考查方向
解题思路
该题解题思路如下
1)利用倍角公式
2)利用特殊角的三角函数求值得到角A,
3)使用正弦定理,进行边角之间的转换
4)根据角的取值范围得到答案
易错点
该题易于忽略了对A的范围的判断,该题属于中档题
已知曲线C的方程是




23.求曲线C的方程;
24.设M(x1,y1),N(x2,y2)是曲线C上两点,向量p=(




正确答案
见解析
解析
解:(1)由题可得:
所以曲线
考查方向
解题思路
1)根据题意联立解方程求出曲线方程
2)写出直线方程,与曲线联立,得到韦达定理
3)根据p·q=0,得到x1,x2的关系
4)解方程得到结果
易错点
本题较简单,一般在计算出错和对p·q=0处理出错
正确答案
见解析
解析
解:
(2)设直线




∴
∴
即
考查方向
解题思路
1)根据题意联立解方程求出曲线方程
2)写出直线方程,与曲线联立,得到韦达定理
3)根据p·q=0,得到x1,x2的关系
4)解方程得到结果
易错点
本题较简单,一般在计算出错和对p·q=0处理出错
为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机抽调了50人,他们年龄的频数分布及支持“生育二胎”人数如下表:
19.由以上统计数据填下面2乘2列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
20.若对年龄在[5,15)的被调查人中各随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?

正确答案
见解析
解析
解:(Ⅰ)2乘2列联表
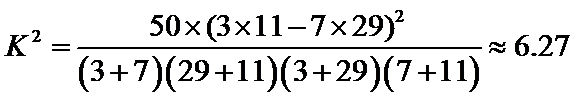
所以没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.
考查方向
解题思路
本题的解题思路
1)根据题意填写表格,并计算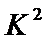
2)对年龄在[5,15)进行区分和分类,写出所有可能
3)利用古典概型求出概率值
易错点
本题第一问易错于计算出错。第二问基本事件空间漏或者重复出错
正确答案
见解析
解析
解:
(Ⅱ)设年龄在[5,15)中支持“生育二胎”的4人分别为a,b,c,d, 不支持“生育二胎”的人记为M,
则从年龄在[5,15)的被调查人中随机选取两人所有可能的结果有:(a,b), (a,c), (a,d), (a, M), (b,c), (b,d),(b, M), (c, d), (c, M),(d, M).
设“恰好这两人都支持“生育二胎””为事件A,
则事件A所有可能的结果有:(a,b), (a,c), (a,d), (b,c), (b,d), (c, d),
∴
所以对年龄在[5,15)的被调查人中随机选取两人进行调查时,恰好这两人都支持“生育二胎”的概率为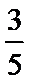
考查方向
解题思路
本题的解题思路
1)根据题意填写表格,并计算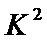
2)对年龄在[5,15)进行区分和分类,写出所有可能
3)利用古典概型求出概率值
易错点
本题第一问易错于计算出错。第二问基本事件空间漏或者重复出错
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,
21.求证:AD⊥平面BFED;
22.已知点P在线段EF上,
正确答案
见解析
解析
(1)在梯形
∵

∴
∴


平面

∴
∴
∴
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
1)根据余弦定理得出BD进而推出
2)由面面垂直得到线面垂直
3)确定PE为体高,进而求出体积
易错点
本题容易在
正确答案
见解析
解析
解:
(2)由(1)知
∵


∴
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
1)根据余弦定理得出BD进而推出
2)由面面垂直得到线面垂直
3)确定PE为体高,进而求出体积
易错点
本题容易在
已知函数f(x)=
25.讨论函数y=f(x)在x∈(m,+∞)上的单调性;
26.若m∈(0,

正确答案
见解析
解析
解:(1)


所以
考查方向
解题思路
本题解题思路
1)借助导函数的性质,直接得出单调区间,
2)根据第一问结论得到转换
3)构造新函数
易错点
本题易错在函数分类讨论不清,
正确答案
见解析
解析
解:
(2)由(1)知
因为


所以下面判断



令


因


所以

使得
所以


所以
所以
即
所以函数

考查方向
解题思路
本题解题思路
1)借助导函数的性质,直接得出单调区间,
2)根据第一问结论得到转换
3)构造新函数
易错点
本题易错在函数分类讨论不清,
选修4—1:几何证明选讲
如图,正方形ABCD边长为2,以A为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结BF并延长交CD于点E.
27.求证:E为CD的中点;
28.求EF·FB的值.
正确答案
见解析
解析
解:(Ⅰ)由题可知



∴

依据切割线定理得
∵圆



同样依据切割线定理得
故
∴

考查方向
解题思路
本题解题思路
1)借助圆的切割定理得出

2)借助等面积求解FC,使用射影定理得到第二问
易错点
本题易错cd是两圆的切线,
正确答案
见解析
解析
解:
(Ⅱ)连结


∴
由
得
又在
考查方向
解题思路
本题解题思路
1)借助圆的切割定理得出

2)借助等面积求解FC,使用射影定理得到第二问
易错点
本题易错cd是两圆的切线,