- 真题试卷
- 模拟试卷
- 预测试卷
1.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.计算
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.某同学设计右面的程序框图用以计算和式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若变量

则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
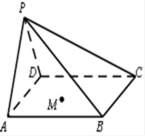
12.四棱锥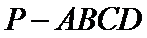
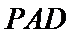
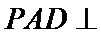
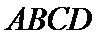
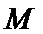
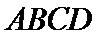

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.某学校开展研究性学习活动,某同学获得一组实验数据如下表:
对于表中数据,现给出以下拟合曲线,其中拟合程度最好的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.一个空间几何体的三视图(单位:

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知向量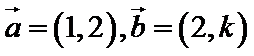
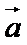
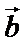
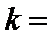
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
15.根据表格中的数据,可以判定函数


正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
16. 设


不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列


(Ⅰ)求数列
(Ⅱ)令



正确答案
(Ⅰ) 当
当
经检验


(Ⅱ)
解析
解析已在路上飞奔,马上就到!
知识点
18.(1)m为何值时,f(x)=x2+2mx+3m+4.有且仅有一个零点;
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围。
正确答案
(1)f(x)=x2+2mx+3m+4有且仅有一个零点⇔方程f(x)=0有两个相等实根
⇔Δ=0,
即4m2-4(3m+4)=0,即m2-3m-4=0,
∴m=4或m=-1.
(2)令f(x)=0,得|4x-x2|+a=0,即|4x-x2|=-a.
令g(x)=|4x-x2|, h(x)=-a.
作出g(x)、h(x)的图象.
由图象可知,当0<-a<4,
即-4<a<0时,g(x)与h(x)的图象有4个交点,即f(x)有4个零点.
故a的取值范围为(-4,0).
解析
解析已在路上飞奔,马上就到!
知识点
19. 在







(I)求角
(II)若

正确答案
(I)由正弦定理得


由于
所以
(II)
因为

所以
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知三棱柱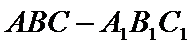
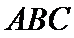
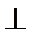


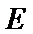

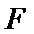
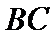
(Ⅰ)求证:直线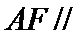

(Ⅱ)求点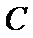

正确答案
(Ⅰ)取

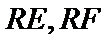
则
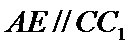

所以四边形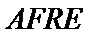
则


(Ⅱ)由等体积法得
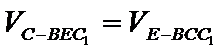
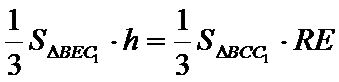
得
解析
解析已在路上飞奔,马上就到!
知识点
21. 某运输公司今年年初用128万元购进一批出租车,并立即投入营运,计划第一年维修、保险及保养费用4万元,从第二年开始,每年所需维修、保险及保养费用比上一年增加4万元,该批出租车使用后,每年的总收入为120万元,设使用

(Ⅰ)写出

(Ⅱ)试确定
正确答案
(Ⅰ)

(Ⅱ) ∵ 
当且仅当

答:该批出租车使用8年后,年平均盈利额达到最大值86万元.
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数
(I)当


(II)在区间



正确答案
(I)当


曲线


所以曲线


(II)解1:
当




故



当

若

若

所以

因此有

解得
这与
当




所以



综上所述,

解2:有已知得:
设







解析
解析已在路上飞奔,马上就到!