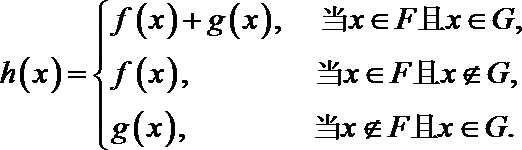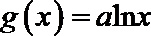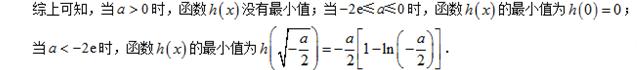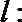- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.下面给出的四个点中,到直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.定义运算:


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.某工厂对一批产品长度进行抽样检测.如图1是根据抽样检测后的产品长度(单位:厘米)数据绘制的频率分布直方图,其中产品长度的范围是[34,44],样本数据分组为[34,36),[36,38),[38,40),[40,42),[42,44],已知样本中产品长度小于38厘米的个数是36,则样本中净重大于或等于36厘米并且小于42厘米的产品的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.给定下列四个命题:
①若两个平面互相垂直,那么分别在这两个平面内的任意两条直线也互相垂直;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③若两个平面平行,则其中一个平面内的直线必平行于另一个平面;
④若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
其中,为真命题的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
12.若关于



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
13.将正整数12分解成两个正整数的乘积有









①
②
③
④
其中正确的序号为_______(填入所有正确的序号).
正确答案
①③
解析
解析已在路上飞奔,马上就到!
知识点
选做题(14~15题,只能从中选做一题)
14.(几何证明选讲选做题)
在梯形










15.(坐标系与参数方程选做题)
设点





正确答案
14.
15.


解析
解析已在路上飞奔,马上就到!
知识点
21.对定义域分别是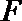
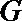
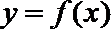
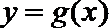
函数
已知函数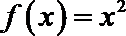
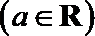
(1)求函数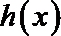
(2)对于实数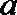
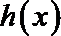
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为
(1)试确定

(2)从40人中任意抽取1人,求此人听觉记忆能力恰为中等,且视觉记忆能力为中等或中等以上的概率.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图1,渔船甲位于岛屿






(1)求渔船甲的速度;
(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.一个几何体是由圆柱









(1)求证:
(2)求三棱锥
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知等差数列{an}的前



(1)求数列
(2)设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.动点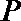
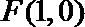

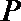
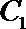
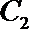
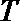
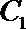
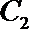
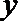
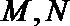
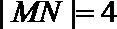
(1)求曲线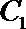
(2)设点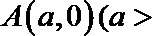
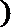
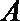
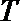
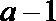
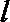
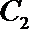
正确答案
解析
解析已在路上飞奔,马上就到!