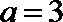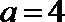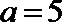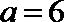- 真题试卷
- 模拟试卷
- 预测试卷
1．已知集合
A
B
C
D
正确答案
解析
由已知得
知识点
2．“2a＞2b”是“lna>lnb”的（ ）
正确答案
解析
“2a＞2b”⇔“a＞b”， “lna＞lnb”⇔“a＞b＞0”，∵“a＞b”是“a＞b＞0”的必要不充分条件，故“2a＞2b”是“lna＞lnb”的必要不充分条件，故选B．
知识点
4．设数列{an}的前n项和为Sn，点
正确答案
解析
因为点
知识点
5．如图，网格纸上小正方形边长为1，粗线是一个棱锥的三视图，则此棱锥的表面积为（ ）
A
B
C
D
正确答案
解析
直观图如图所示四棱锥
故此棱锥的表面积为
知识点
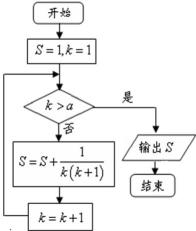
7．某程序框图如图所示,若该程序运行后输出的值是
A
B
C
D
正确答案
解析
第一次：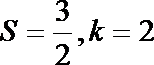
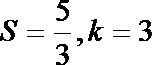
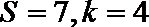
知识点
8．已知
A
B
C
D2
正确答案
解析
不等式表示的可行域如图所示，把目标函数
得
知识点
11．定义域为
A
B
C
D
正确答案
解析
构造函数
所以
知识点
3．设
A
B
C0
D-l
正确答案
解析
由题意得：
知识点
9．设
A
B
C
D
正确答案
解析
由条件得： 
知识点
10．设
A
B
C
D
正确答案
解析
不妨设圆与
知识点
12．在平面直角坐标系xoy中，已知△ABC的顶点A(－6，0)和C(6，0)，顶点B在双曲线
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．在长方体
A
B
C
D
正确答案
解析
如图，过
知识点
13．设
正确答案
解析
以
知识点
15．设函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．已知
正确答案
解析
知识点
16．设数列
正确答案
解析
由题意可得，
∴数列
知识点
17．已知函数
（Ⅰ）当
（Ⅱ）设
正确答案
解：
（Ⅰ）当
（Ⅱ）
由题意，
令
故
函数
解析
解析已在路上飞奔，马上就到！
知识点
19．某班主任对全班50名学生学习积极性和参加社团活动情况进行调查，统计数据表
（1）如果随机从该班抽查一名学生，抽到参加社团活动的学生的概率是多少？抽到不参加社团活动且学习积极性一般的学生的概率是多少？
（2）运用独立检验的思想方法分析：学生的学习积极性与参加社团活动情况是否有关系？并说明理由．
正确答案
解：
（1）随机从该班抽查一名学生，抽到参加社团活动的学生的概率是
（2）∵
∴有
解析
解析已在路上飞奔，马上就到！
知识点
20．已知椭圆
（1）求椭圆
（2）是否存在一定点
正确答案
解：
（1）设椭圆的方程为
由①②可得
（2）过点
则
解得
下证
设过点
解析
解析已在路上飞奔，马上就到！
知识点
18．如图，矩形
（1）求证：
（2）求三棱锥
正确答案
解：
（1）证明：
∴
（2）
∴
∴
解析
解析已在路上飞奔，马上就到！
知识点
21．设
（1）求
（2）求证：当
正确答案
解：
（1）由f(x)＝ex－2x＋2a，x∈R知f′(x)＝ex－2，x∈R.令f′(x)＝0，得x＝ln 2.[:]
于是当x变化时，f′(x)，f(x)的变化情况如下表：
故f(x)的单调递减区间是(－∞，ln 2)，单调递增区间是(ln 2，＋∞)，f(x)在x＝ln 2处取得极小值，
极小值为
（2）设
于是
由(1)知当
于是对任意x∈R都有g′(x)＞0，
所以g(x)在R内单调递增．
于是当
而g(0)＝0，从而对任意
即
解析
解析已在路上飞奔，马上就到！
知识点
选做题：青葱22、23、24三题中任选一题做答，如果多做，则按第一题计分。
22．选修
如图，
（Ⅰ）证明：
（Ⅱ）证明：
23．选修4－4
在直角坐标系
（Ⅰ）求圆
（Ⅱ）若将圆
24． 选修4－1
解关于
（Ⅰ）当
（Ⅱ）设函数
正确答案
22.
（Ⅰ）∵ 
又∵
又
（Ⅱ）由（Ⅰ）有
又
23.
（Ⅰ）圆
得
（Ⅱ）将圆
经过伸缩变换
设
所以当
24．
（Ⅰ）原不等式可化为
又原不等式解集为
即
所以
（Ⅱ）
故令
解析
解析已在路上飞奔，马上就到！