- 真题试卷
- 模拟试卷
- 预测试卷
5.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数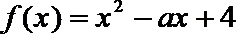
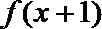
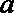
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.下列说法错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.对于函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数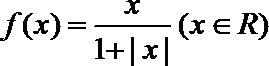
(1)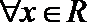
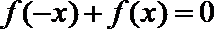
(2)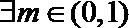
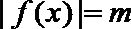
(3)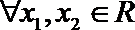
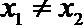
(4)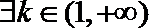
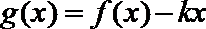
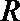
正确答案
(1)(2)(3)
解析
解析已在路上飞奔,马上就到!
知识点
15.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知集合





正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
12.定义在




正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
17.已知幂函数

(1)求函数
(2)设函数



正确答案
(1)幂函数
且在区间

又

(2)
由题,
解析
解析已在路上飞奔,马上就到!
知识点
19.某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和后期会因供应不足使价格呈持续上涨态势,而中期又将出现供大于求,使价格连续下跌.现有三种价格模拟函数:①




(1)为准确研究其价格走势,应选哪种价格模拟函数(不必说明理由)
(2)若





(3)在(2)的条件下研究下面课题:为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌。
正确答案
(1)根据题意,应选模拟函数
(2)

所以
(3)
令
又



所以可以预测这种海鲜将在9月,10月两个月内价格下跌.
解析
解析已在路上飞奔,马上就到!
知识点
20.在


(1)求证:
(2) 若

正确答案
(1)由 

即
整理得:
所以
又
所以
(2)由(1)及

又
所以
所以三角形ABC的面积
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)若函数


(2)记函数



正确答案
(1) 
∴

令
∵
∴
∴
(2)
∵
易知

∴
∴
令




则
解得
解析
解析已在路上飞奔,马上就到!
知识点
16.定义域为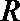
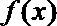
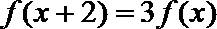
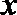
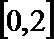
(1)当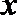
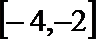
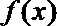
(2)当x∈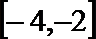
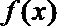
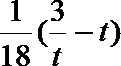
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数





(1)求

(2)若不等式


正确答案
(1)
因为


故

(2)由已知可得
所以

化为


因

记


所以

解析
解析已在路上飞奔,马上就到!