- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合


正确答案
解析
由




考查方向
解题思路
1.先根据
易错点
不知道
知识点
2.已知复数




正确答案
解析
由题意可得,



考查方向
解题思路
1.先利用复数的运算法则化简复数; 2.根据纯虚数的概念即可得到方程后解方程即得答案。
易错点
1:不理解纯虚数是什么; 2复数运算出错。
知识点
3.执行如图所示的程序框图,若输入的


正确答案
解析
执行程序框图,第一次





考查方向
解题思路
根据给出的程序框图循环执行,后满足条件跳出循环即可。
易错点
1.无法确定程序结束的条件导致出错;2.不将程序运行完成就退出程序导致出错。
知识点
5.已知具有线性相关关系的两个变量
且回归直线方程为


正确答案
解析
由题意可得,







考查方向
解题思路
1.先求出样本点的中心

易错点
1.不理解回归直线部分的基础知识,导致不知道该干什么;2.数据计算出错。
知识点
6.函数
正确答案
解析
由题意可得,





考查方向
解题思路
1.根据函数的解析式确定其奇偶性,排除A,C;2.利用图像知当

易错点
1.不会利用图形中的信息;2.不知道该用函数的什么性质去解决。
知识点
4.设


正确答案
解析
由题意可得,“





考查方向
解题思路
先将题中的结论

易错点
1.不会转化题中的结论
知识点
7.已知函数

正确答案
解析
由题意可得,


考查方向
解题思路
1.先判断

易错点
1.不会指数恒等式

知识点
8.某几何体的三视图如图所示,则该几何体外接球的表面积为( )
正确答案
解析
由三视图可知,该几何体是底面半径为





考查方向
解题思路
1.先由题中给出的三视图判断出其直观图;2.利用图中给出的数据求其外接球的半径和表面积。
易错点
1.空间想象能力较弱,无法正确判断出其直观图的形状;2.对于几何体与球的切接问题不会处理。
知识点
10.对于两个平面向量



正确答案
解析
因为













考查方向
解题思路
.根据题中给出的运算公式分别带入选项逐个判断正误。
易错点
1.不会利用题中给出的新定义;2.对于新定义和我们学过的知识如何如何结合存在障碍。
知识点
9.已知函数




正确答案
解析
构造函数








考查方向
解题思路
1.先构造函数

易错点
1.不会利用题中给出的导数的等式构造函数;2.不知道选项中给出的两个数什么关系。
知识点
11.函数
正确答案
解析
由题意可得



考查方向
解题思路
1.根据函数有意义,得到不等式组;2.解题中给出的不等式组即可。
易错点
1.解不等式
知识点
15.抛物线







正确答案

解析
由题意可知,双曲线

















考查方向
解题思路
1.先根据题中给出的方程求出题中需要的基本量;2.设出点M的坐标后利用斜率相等求出




易错点
1.不会利用导数的几何意义表示切线的斜率;2.找不到题中给出的条件
知识点
14.某企业生产甲、乙两种产品均需用




正确答案

解析
设每天生产甲、乙产品分别为










考查方向
解题思路
1.设出变量后列出变量满足的约束条件
易错点
1.不会根据题意设变量表示题中的约束条件;2.不会利用线性规划求目标函数的最值。
知识点
12.若直线


正确答案

解析
圆









考查方向
解题思路
1.先将圆的方程化为标准方程,导出圆心;2.将圆心坐标带入直线方程得到等式
易错点
不会将

知识点
13.设△




正确答案

解析
由








考查方向
解题思路
1.先根据正弦定理将角间的关系转化为边
易错点
不会将题中的条件
知识点
某市为庆祝北京夺得











16.若电视台记者要从抽取的群众中选


17.已知第




正确答案
(Ⅰ)
解析
(Ⅰ)设第



被采访人恰好在第


∴估计被采访人恰好在第

考查方向
解题思路
根据题中给出的频率分布直方图求出第(1)问的答案;
易错点
列基本事件的个数时多数或少数。
正确答案
(Ⅱ)
解析
(Ⅱ)第


∴第


记第




从第



至少有一名女性群众包含
共
∴从第



考查方向
解题思路
求出各组中的群众人数,后数出所有的基本事件的个数和事件 至少有一名女性群众所包含的基本事件的个数相除即可。
易错点
列基本事件的个数时多数或少数。
已知函数

18.求
19.将函数






正确答案
(Ⅰ)
解析
(Ⅰ)原函数可化为

∵函数

∴

∴

∴

考查方向
解题思路
.先根据三角恒等变换将函数


易错点
化简函数
正确答案
(Ⅱ)
解析
(Ⅱ)由(Ⅰ)知,







∴
∵

∵函数


∴实数

考查方向
解题思路
根据图像变换求出函数
易错点
化简函数
已知函数
24.当

25.当

26.若对于任意的


正确答案
(Ⅰ)当


解析
(Ⅰ)当




当



当



∴当


考查方向
解题思路
直接求导,判断导数的正负后即可得到极值;
易错点
无
正确答案
(Ⅱ)当



当


当



解析
(Ⅱ)当




由



(1)当




(2)当


(3)当



在
综上所述,
当



当


当



考查方向
解题思路
求导后分类讨论导数的正负后确定函数的单调区间;
易错点
在求函数的单调性时,不会确定分类的标准;
正确答案
(Ⅲ)
解析
(Ⅲ)由(Ⅱ)知,当


∴
∵对于任意的

∴

∴

当


∴实数

考查方向
解题思路
先根据第(2)问放缩后构造不等式
易错点
不会放缩
如图,在三棱柱





20.求证:

21.求证:平面

正确答案
(Ⅰ)略.
解析
(Ⅰ)连接



在三棱柱
四边形


又∵


又∵



∴

考查方向
解题思路
先根据题中给出的条件证明
易错点
不会从图中找与直线
正确答案
(Ⅱ)略.
解析
(Ⅱ)∵



∵


∵



∵





∵

∵




∴

∵

∴平面

考查方向
解题思路
先证明

易错点
找不到哪条线垂直于那个平面导致根本没有思路。
已知等比数列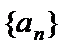
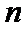
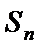
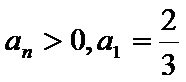
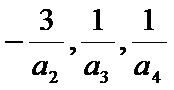
22.求数列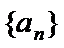
23.设数列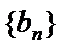
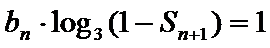
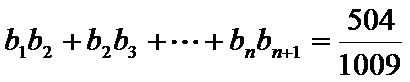
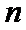
正确答案
(Ⅰ)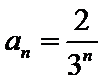
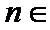

解析
(Ⅰ)设等比数列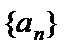
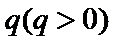
∵ 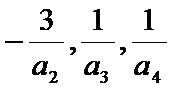
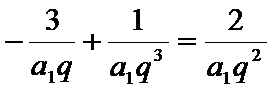
∴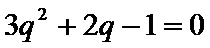
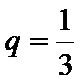
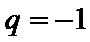
∴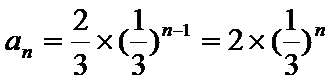
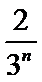
∴数列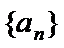
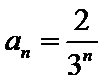
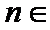

考查方向
解题思路
先根据题中给出的条件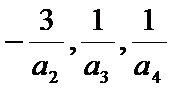
易错点
对于题中给出的条件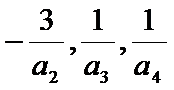
正确答案
(Ⅱ)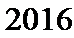
解析
(Ⅱ)由(Ⅰ)知,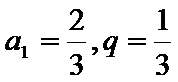
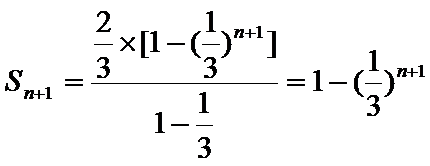
∵数列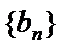
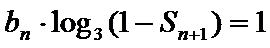
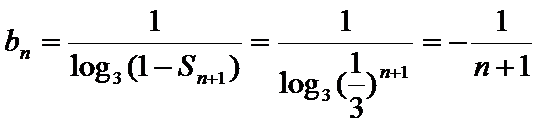
∴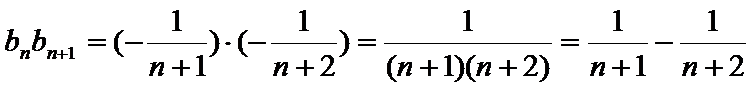
∴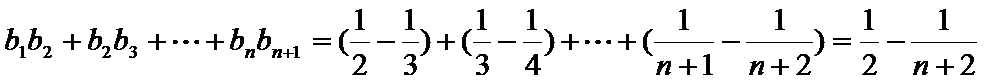
由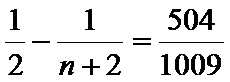
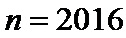
∴满足方程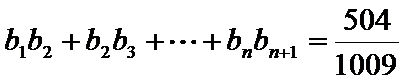
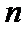
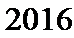
考查方向
解题思路
1.先根据题中给出的条件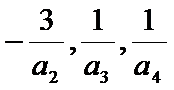
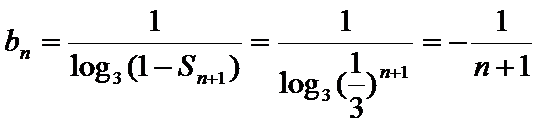
易错点
1.对于题中给出的条件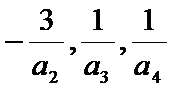
已知椭圆


27.求椭圆
28.设椭圆









(i)求证:线段

(ii)求
正确答案
(Ⅰ)
解析
(Ⅰ)设椭圆


∵椭圆


由

∴椭圆

考查方向
解题思路
直接根据椭圆的基本量直接带入求解即可;
易错点
在运算时算数出错;
正确答案
(Ⅱ)(i)略;(ii)
解析
(Ⅱ)(i)由(Ⅰ)知,椭圆


(1)当直线












(2)当直线











设



由

判别式

则

由




∴直线


∴线段

(ii)(1)当直线


∴

(2)由(i)知直线






令
则




此时


考查方向
易错点
不会构造函数
【解题思路
第(1)小问先求出线段

第(2)问先求





























































