文科数学柳州市2015年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．已知集合，且，若，则（）

D-

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域及其求法

题型：单选题

分值: 5分

6．设为平面，为直线，给出下列条件：

①

②

③

④

基中能能的条件是（）

A①②

B②③

C②④

D③④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

5．为得到函数的图象，只需将函数的图象（）

A向左平移个长度单位

B向右平移个长度单位

C向左平移个长度单位

D向右平移个长度单位

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

8．正三棱锥底面边长为，侧棱与底面成角，则正三棱锥外接球面积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数单调性的应用

题型：单选题

分值: 5分

12．已知椭圆了为椭圆的左．右焦点，是椭圆上任一点，若的取值范围为，则椭圆方程为（）

AA．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数图象及其与指数的关系

题型：单选题

分值: 5分

3．若二项式的展开式的第五项是常数项，则自然数的值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

2．已知关于的不等式的解集为，则等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相等向量与相反向量

题型：单选题

分值: 5分

4．己在等差数列的公差，若，则该数列的前项和的最大值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

9．设，函数的导函数是)，若是偶函数，则曲线在原点处的切线方程为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：单选题

分值: 5分

7．己知关于直线对称，则的最小值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

10．将编号为的五个球放入编号为的五个盒子，每个盒子放一个球，若恰好有两个球的编号与盒子编号相同，则不同的投放方法有（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

11．若，则的取值范围为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

15．若点到直线的距离为，且该点在不等式所确定的平面区域内，则___________。

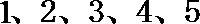
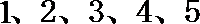
正确答案

-3

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

14．在中，已知是边上一点，，则___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 5分

13．已知，则_________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

分值: 5分

16．设椭圆 (．为常数且)，和轴正方向交于点，和轴正方向交于点，为第一象限内椭圆上的点，则四边形面积在最大值为___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

18．甲、乙两队在进行一场五局三胜制的排球比赛中，规定先赢三局的队获胜，并且比赛就此结束，现已知甲．乙两队每比赛一局，甲队获胜的概率是，乙队获胜的概率是，且每局比赛的胜负相互独立。

（1）求甲队以获胜的概率；

（2）求乙队获胜的概率。

正确答案

解：

（1）甲队以获胜，说明前四局，第五局甲胜，

∴甲队以获胜的概率，

（2）乙队获胜的情况有三种，

∴乙队获胜的概率

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：简答题

分值: 10分

17．已知函数，且的最大值为，其图象相邻两对称轴之间的距离为，并过点.

（1）求函数的解析式；

（2）求。

正确答案

解：

（1）

的最大值为，即

又∵相邻对称轴之间的距离为

由于在图像上，，即，

，即

（2）

，

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的定义域

题型：简答题

分值: 12分

20．在数列中，(，且)

（Ⅰ）求的值；

（Ⅱ）证明：数列是等比数列，并求的通项公式；

（Ⅲ）求数列的前项和。

正确答案

解：

（Ⅰ）

（Ⅱ）

以为首项，为公比的等比数列

从而，即

（Ⅲ）当为偶数时，

当为奇数时，

综上，

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 12分

22．已知曲线上任意一点到直线的距离与它到点的距离之比是。

（I）求曲线的方程；

（II）设为曲线与轴负半轴的交点，问：是否存在方向向量为的直线，与曲线相交于两点，使，且与夹角为?若存在，求出值，并写出直线的方程；若不存在，请说明理由。

正确答案

解：

（Ⅰ）设为曲线上任意一点，依题意

化简：，为椭圆，其方程为

（Ⅱ）设直线，由消去得：

设，中点，

则，

………（1）

依题意：，与夹角为，为等边三角形，

，即，………（2）

由（2）代入（1）：，

又为等边三角形，到距离，

即，

解得：即，经检验方程有解，

所以直线的方程为：

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 12分

21．已知函数。

（Ⅰ）求函数的极值；

（Ⅱ）若对任意的都有，求实数的取值范围。

正确答案

解：

（Ⅰ）

令得，

当变化时，及变化如下图表

∴当时取极大值，当时取极小值

（Ⅱ）设

（1）当时，恒成立，此时成立，

即成立，

（2）当时，由得

当，即在为减函数

当，即在为增函数

在时，，

即，解得

综上：的取值范围是

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 12分

19．已知矩形中，，将沿折起，使点在平面内的射影落在上。

（Ⅰ）求证：平面平面；

（Ⅱ）求点到平面的距离；

（Ⅲ）若为中点，求二面角的大小。

正确答案

证明：

（Ⅰ）∵点在平面上的投影落在上，

即平面经过平面的垂线，∴平面平面

（Ⅱ）如图所示建立空间直角坐标系，则

∵的投影在上，令由即

，由，

求得平面的一个法向量为，

而，∴到平面的距离为

（Ⅲ）由，求得平面的一个法向量

，求得平面的一个法向量

由图可见为锐二面角，设此平面角为，则

解析

解析已在路上飞奔，马上就到！

知识点

分式不等式的解法

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷