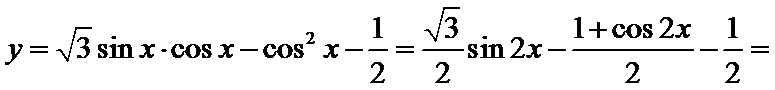- 真题试卷
- 模拟试卷
- 预测试卷
2.在等差数列



正确答案
解析
由

考查方向
解题思路
根据两个已知条件列方程组,即可求出公差d。
易错点
对等差数列的通项公式及求和公式不熟悉导致出错。
知识点
4.设


正确答案
解析
由



考查方向
解题思路
直接根据相关定理进行判断。
易错点
空间点线面的位置关系、线线、线面、面面平行与垂直的相关定理不熟悉导致出错。
知识点
7.已知函数


①

②当


③当

④
其中正确的是( )
正确答案
解析
由图像可知函数的值域为











考查方向
解题思路
先画出函数
易错点
不能准确画出函数的图像导致本题出错。
知识点
6.若实数


正确答案
解析
画出不等式组




考查方向
解题思路
根据约束条件画出可行域,作出直线
易错点
不知道目标函数的几何意义导致本题出错。
知识点
1.已知全集



正确答案
解析
易知

考查方向
解题思路
先求集合B在全集U中的补集,再求交集。
易错点
忽略集合中元素的互异性导致出错。
知识点
3. “


正确答案
解析
由直线








考查方向
解题思路
先根据两直线平行的等价条件按求出参数a,再进行判断。
易错点
对两直线平行的等价条件不熟悉导致出错。
知识点
5.要得到函数

正确答案
解析
将函数





考查方向
解题思路
先将函数

易错点
三角函数相位变换公式不熟悉导致出错。
知识点
8.如图,焦点在












正确答案
解析
如右图所示,设另外两个切点分别为M,N,由




考查方向
解题思路
根据切线长相等及椭圆的定义先求出实数a,进而求出椭圆的离心率。
易错点
不知如何利用已知信息导致本题没有思路。
知识点
9.

正确答案

解析
试题分析:依题意可知


考查方向
解题思路
直接运用指数与对数的运算律进行计算。
易错点
指数与对数的运算公式不熟悉导致出错。
知识点
10.双曲线


正确答案
6,
解析
试题分析:依题意可知双曲线的标准方程为





考查方向
解题思路
化双曲线方程为标准方程,直接求出实轴长及渐近线方程,利用直线与圆相切即可求出实数m的值。
易错点
相关知识点不熟悉导致出错。
知识点
11.某几何体的三视图如图所示,则该几何体的体积等于 ,表面积等于 .
正确答案

解析
试题分析:依题意可知该几何体为底面半径为2,高为3 的圆柱的一半,所以该几何体的体积为



考查方向
解题思路
由三视图还原出原图后即可求该集合体的表面积与体积。
易错点
不能由三视图还原出原图导致出错。
知识点
15.已知正实数



正确答案
解析
试题分析:依题意可知


考查方向
解题思路
现对所给函数是进行化简,再变形求最值。
易错点
不知如何对所给式子进行化简导致出错。
知识点
12.在边长为1的等边





正确答案

解析
试题分析:由






考查方向
解题思路
直接运用三点共线的结论及向量的运算律进行计算。
易错点
忽视向量的夹角导致数量积求错。
知识点
13.函数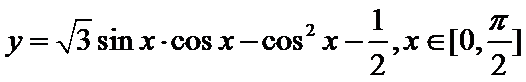
正确答案
解析
试题分析:依题意可知
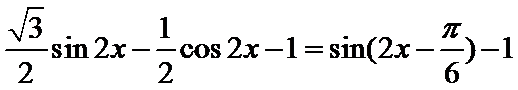
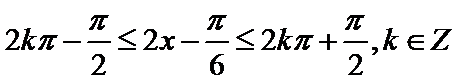
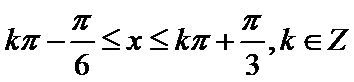
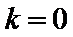
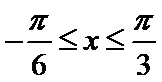
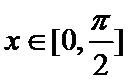
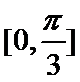
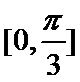
考查方向
解题思路
先化简函数解析式,再求单调区间。
易错点
化简函数解析式时因对三角恒等变换共识不熟悉导致出错。
知识点
14.已知









正确答案
解析
试题分析:依题意可知













考查方向
解题思路
准确理解题中所给的新概念,然后运用其进行计算。
易错点
不能理解新概念导致出错。
知识点
已知函数

24.若




25.若函数



正确答案

解析
试题分析:本题属于分段函数的性质、函数的最值、函数的单调性的综合应用问题,属于拔高题,不易得分,解析如下:当
结合图象可知,
函数在





即

考查方向
解题思路
先求出函数

易错点
第二问中忽略对实数a范围的讨论导致出错。
正确答案


解析
试题分析:本题属于分段函数的性质、函数的最值、函数的单调性的综合应用问题,属于拔高题,不易得分,解析如下:
(1)若


(2)若


在

故



(3)若
结合图象,有以下三种情况:
当








当




所以


③当






考查方向
解题思路
根据题中条件就参数a的范围进行分类讨论,结合函数


易错点
第二问中忽略对实数a范围的讨论导致出错。
在




16.求
17.若


正确答案

解析
试题分析:本题属于向量的坐标运算、正余弦定理及三角形的面积公式的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:因为





考查方向
解题思路
利用向量

易错点
相关知识点不熟容易处错。
正确答案

解析
试题分析:本题属于向量的坐标运算、正余弦定理及三角形的面积公式的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
由余弦定理得,
化简得,




故

考查方向
解题思路
利用余弦定理求出a边,在利用面积公式即可求出

易错点
相关知识点不熟容易处错。
如图,








18.求证:
19.当三棱锥






正确答案
见证明.
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:证明:因为






考查方向
解题思路
直接利用线面垂直的判定定理进行证明;
易错点
相关知识不熟容易处错。
正确答案
不存在.
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:不存在.
证明如下:
当面




所以

(方法一)连结
因为

所以









设




因为

(方法二)(前面同解法一)在直角三角形






(方法三)已证得

则









考查方向
解题思路
本问题方法较多,可以直接进行证明,也可以利用向量进行证明,详见解析.
易错点
相关知识不熟容易处错。
已知正项数列




20. 求
21. 若



正确答案

解析
试题分析:本题属于数列知识的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:因为
所以当





所以







所以
考查方向
解题思路
直接利用

易错点
相关知识点不熟容易处错。
正确答案

解析
试题分析:本题属于数列知识的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:由已知及(Ⅰ)知,


②



考查方向
解题思路
先求出
易错点
相关知识点不熟容易处错。
已知









22. 求动点
23.设22题中的轨迹与






正确答案
解析
试题分析:本题属于直线与圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:焦点













考查方向
解题思路
利用相关知识求抛物线方程;
易错点
对题中条件不知如何处理导致出错。
正确答案
直线:
解析
试题分析:本题属于直线与圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:由已知及22题知,
因为








当且仅当




考查方向
解题思路
根据题中条件求出面积,再利用均值不等式求出面积的最值.
易错点
对题中条件不知如何处理导致出错。