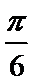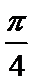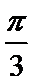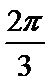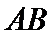- 真题试卷
- 模拟试卷
- 预测试卷
2.复数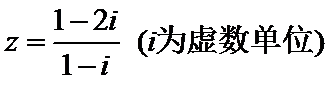
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知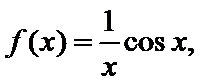
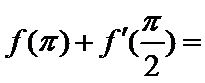
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知命题

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在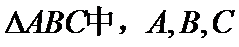
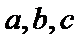
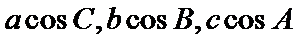
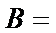
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知正三角形






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知平面内一点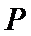
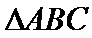
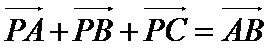
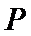
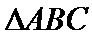
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知对数函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.定义方程





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知角



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.一空间几何体的三视图如图所示,则该几何体的体积为__________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在区间


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知

正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
18.一个袋中装有四个形状大小完全相同的球,球的编号分别为
(Ⅰ)从袋中随机取出两个球,求取出的球的编号之和不大于
(Ⅱ)先从袋中随机取一个




正确答案
(Ⅰ)从袋子中随机取两个球,其一切可能的结果组成的基本事件有:
1和2,1和3,1和4,2和3,2和4,3和4共6个。
从袋中随机取出的求的编号之和不大于4的事件共有1和2,1和3两个。
因此所求事件的概率为
(II)先从袋中随机取一个球,记下编号为m;
放回后,再从袋中随机取一个球,记下编号为n,
其一切可能的结果(m,n)有:
(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)(3,1)(3,2)(3,3)(3,4)(4,1)(4,2)(4,3)(4,4),共16个
有满足条件n≥m+2n的时间的概率为
故满足条件n<m+2的事件的概率为
解析
解析已在路上飞奔,马上就到!
知识点
20.某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为



(1)写出年利润L(万元)关于年产量x(千件)的函数解
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在三角形ABC中,∠A,∠B,∠C的对边分别为
(1)求∠A;
(2)若

正确答案
(1)由余弦定理知:cosA=
∴ ∠A=
(2)由正弦定理得:
∴ b=2sinB,c=2sinC
∴ b2+c2=4(sin2B+sin2C)=2(1-cos2B+1-cos2C)
=4-2cos2B-2cos2(
=4-2cos2B-2cos(
=4-2cos2B-2(-

=4-cos2B+

又∵ 
∴ 


∴ 

∴ 3<b2+c2≤6
解析
解析已在路上飞奔,马上就到!
知识点
19.如图所示,在四棱锥P—ABCD中,平面
(1)设M是PC上的一点,求证:平面MBD⊥平面PAD;
(2) 求四棱锥P—ABCD的体积
正确答案
(1)证明:
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(Ⅰ)若

(Ⅱ)若



(Ⅲ)若

正确答案
(Ⅰ)因为
令


所以
(由



(Ⅱ)因为
因为


所以
只要

(Ⅲ


当


所以当

当



在
所以当


当




所


当


在


又
当


当


当



综上所述,
当

当

当



当



解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列


(1)求证数列

(2)求数列





正确答案
(1)∵
∴ 

∴ 数列
∴ 
(2)∵ 
∴
∵
又
∴ 

∴ 当

要使得

结合(1)的结果,只需
∴ 正整数
解析
解析已在路上飞奔,马上就到!