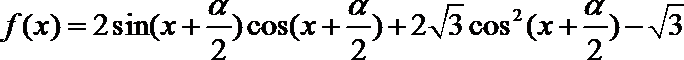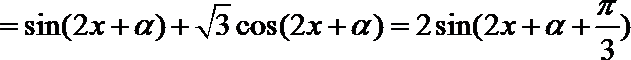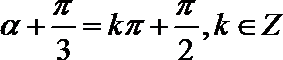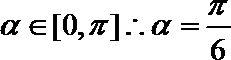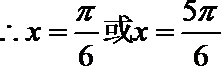- 真题试卷
- 模拟试卷
- 预测试卷
2.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知直线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若椭圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数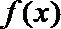
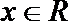
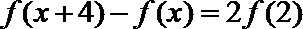
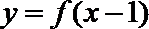
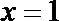
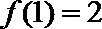
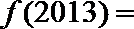
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.曲线



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
12.设


正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
13.已知










正确答案
71
解析
解析已在路上飞奔,马上就到!
知识点
14.如图,一个空间几何体的正视图、侧视图都是面积为

正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
15.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,在直三棱柱




(1) 求证:

(2) 求证:

正确答案
解:
(1)因为在直三棱柱


因为


又



因为
又因为


又


(2)在正方形





结



因为





解析
解析已在路上飞奔,马上就到!
知识点
16.已知函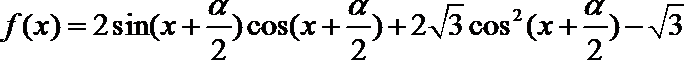
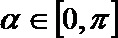
(Ⅰ)求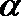
(Ⅱ)若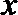
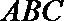
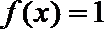
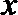
正确答案
(Ⅰ)
由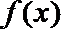
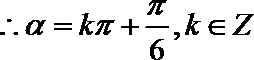
(Ⅱ)由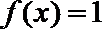
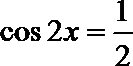
解析
解析已在路上飞奔,马上就到!
知识点
18.数列




(Ⅰ)求数列
(Ⅱ)设



正确答案
解:(Ⅰ)由已知:对于

∴
①-②得
∴
∵

∴数列
又n=1时,

∴

(Ⅱ) 解:由(1)可知
解析
解析已在路上飞奔,马上就到!
知识点
20. 设函数
(Ⅰ)若

(Ⅱ)若

正确答案
解:(Ⅰ)


当



所以


故
(Ⅱ)若



由



由



所以,

所以

解析
解析已在路上飞奔,马上就到!
知识点
21.已知







(Ⅰ)求
(Ⅱ)一动圆过点


(Ⅲ)过点





正确答案
解:(Ⅰ)

所以AC边所在直线的方程为

由


又
所以

(Ⅱ)设动圆圆心为



所以

故点



从而动圆圆心的轨迹方程

(Ⅲ)

由

故
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,PA垂直于矩形ABCD所在的平面,
(Ⅰ)求证:平面PCE 
(Ⅱ)求三棱锥P-EFC的体积.
正确答案
解:
(Ⅰ)
(Ⅱ)由(2)知
解析
解析已在路上飞奔,马上就到!