- 真题试卷
- 模拟试卷
- 预测试卷
1.若全集
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数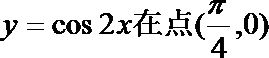
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设向量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.命题“设a、b、
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.“α,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.要得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知命题p:不等式



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.对于在区间










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在等差数列


正确答案
14
解析
解析已在路上飞奔,马上就到!
知识点
17.在


(1)求角的大小;
(2)设


正确答案
(1)由
由正弦定理,得
即
在

(2)
所以
令
得

即当


解析
解析已在路上飞奔,马上就到!
知识点
18.在


(1)若
(2)若


正确答案
(1)由
即
解得:
而
可以变形为
即
所以
(2)由(1)知 
则
又
所以
即
当且仅当
故
解析
解析已在路上飞奔,马上就到!
知识点
20.已知等比数列


(1)求
(2)设
正确答案
(1)依题意
即

(2)
解析
解析已在路上飞奔,马上就到!
知识点
21.设关于的方程

(1)证明:

(2)当为何值时,

正确答案
(1)证明:
由方程




所以

(2)解:由(1)知在


最大值为


可求得

故当


且
解析
解析已在路上飞奔,马上就到!
知识点
19.某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式
(2)该企业已筹集到10万元资金,并全部投入到A,B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元
正确答案
(1)投资为万元,
A产品的利润为

由题设



由图知

又
从而



(2)设B产品投入万元,
则A产品投入10-万元,设企业的利润为万元
则
=

当

此时
当A产品投入

企业获得最大利润为
解析
解析已在路上飞奔,马上就到!
知识点
22.已知过函数

(1)求
(2)求的取值范围,使不等式

(3)令


正确答案
(1)

依题意得
∴

把

∴
(2)令

∵
∴
要使不等式


∴
(3)
∴
∵
∴
①当

∴ 


得
②当

令
得


∴
∴
∴
③当

∴

∴

∴存在一个


解析
解析已在路上飞奔,马上就到!