文科数学西城区2014年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共8小题，每小题5分，共40分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

4．定义：。若复数z满足，则z等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：单选题

分值: 5分

5．函数在点处的切线是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

1．tan（－30）°的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

2．已知向量，若∥，则实数（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

3．已知集合A、B均为全集的子集，且，则（）

A{3}

B{4}

C{3，4}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

6．公比为2的等比数列的各项都是正数，且，则＝（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

分值: 5分

7．设、都是非零向量，下列四个条件中，使成立的充分条件是（）

B∥

D∥且＝

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

题型：单选题

分值: 5分

8．若函数（a、b为常数，）在处取得最小值，则函数是（）

A偶函数且它的图象关于点对称

B偶函数且它的图象关于点对称

C奇函数且它的图象关于点对称

D奇函数且它的图象关于点对称

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域及其求法

填空题本大题共6小题，每小题5分，共30分。把答案填写在题中横线上。

题型：填空题

分值: 5分

9．设函数的定义域是，则函数的定义域是________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

12．点A（－1，－2）在直线上，若，则的最小值为________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化

题型：填空题

分值: 5分

10．若曲线在点（1，2）处的切线经过坐标原点，则＝_______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义恒过定点的直线

题型：填空题

分值: 5分

14．直角坐标系中，两定点。动点满足，则点P构成的区域的面积是________；点构成的区域的面积是________。

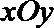
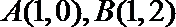
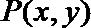
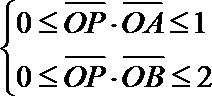
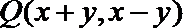
正确答案

2，4

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：填空题

分值: 5分

13．若非零向量满足，则与的夹角为_________。

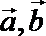
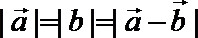
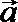
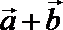
正确答案

30°

解析

解析已在路上飞奔，马上就到！

知识点

向量的模平面向量数量积的运算数量积表示两个向量的夹角

题型：填空题

分值: 5分

11． △ABC中，内角A，B，C所对的边长分别为，如果A＝60°，AC＝3，面积为，那么BC的长度为________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

余弦定理

简答题（综合题）本大题共80分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 13分

15．已知：向量，

（1）若，求x的值；

（2）设函数，求的最大值。

正确答案

（1）由，

由，得；

（2）

，

∴当，即时，。

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 13分

18．已知，函数。

（1）当时，求曲线在点处的切线方程；

（2）求在区间上的最小值。

正确答案

（1）当时，，，

所以，因此。

即曲线在点处的切线斜率为。，

所以曲线在点处的切线方程为，

即。

（2）因为，所以。

令，得。

①若，则，在区间上单调递增，此时函数无最小值。

②若，当时，，函数在区间上单调递减，

当时，，函数在区间上单调递增，

所以当时，函数取得最小值。

③若，则当时，，函数在区间上单调递减，

所以当时，函数取得最小值。

综上可知，当时，函数在区间上无最小值；

当时，函数在区间上的最小值为；

当时，函数在区间上的最小值为。

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义利用导数研究函数的单调性利用导数求函数的最值直线的一般式方程

题型：简答题

分值: 13分

16．已知：函数满足，函数，

（1）求函数的表达式；

（2）若，求x的取值范围。

正确答案

（1）令，则，

。

即

（2），

，

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：简答题

分值: 13分

17．已知：△ABC中的内角A，B，C所对的边长分别为，且，

（1）当时，求角A的大小；

（2）求△ABC面积的最大值。

正确答案

（1）因为，所以。

因为，由正弦定理可得

因为，所以A是锐角，所以30°。

（2）因为△ABC的面积，

所以当ac最大时，△ABC的面积最大。

因为，所以。

因为，所以，

所以，（当时等号成立）

所以△ABC面积的最大值为3。

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用

题型：简答题

分值: 14分

19．已知：首项为的等比数列的前n项和为，且、、成等差数列，

（1）求数列的通项公式；

（2）证明。

正确答案

（1）设等比数列的公比为q，

、、成等差数列，，即，可得，

于是，又，则数列的通项公式；

（2）证明：，

当n为奇数时，随n的增大而减小，所以；

当n为偶数时，随n的增大而减小，所以，

则对于，有。

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：简答题

分值: 14分

20．已知：函数，

（1）设，证明在区间内存在唯一的零点；

（2）设，若对任意，有，求实数b的取值范围；

（3）在（1）的条件下，设是在内的零点，判断数列的增减性。

正确答案

（1）当时，，

在区间内存在零点，

∵当时，在区间上是增函数，

在区间内存在唯一的零点。

（2）当时，，

对任意，有等价于在的最大值与最小值的差，

①当，即时，在上是增函数，

，不合题意；

②当，即时，，＝

，满足题意；

③当，即时，＝

，满足题意；

④当，即时，在上是减函数，

，不合题意；

综上所述：当时，满足题目要求。

（3），设是在区间内唯一的零点，

则有；，

，且在区间上是增函数，

数列是递增数列。

又证：是在区间内唯一的零点，

，

的零点在区间内，

即数列是递增数列。

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷