- 真题试卷
- 模拟试卷
- 预测试卷
2.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知倾斜角为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在等差数列{




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如下图,某简单几何体的正(主)视图与侧(左)视图都是边长为1的正方形,且其体积为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
14.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设

①若


②若
③若
④若
其中正确命题的序号是______________(把所有正确命题的序号都写上).
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
19.如图所示,直角梯形ACDE与等腰直角

(1)求证:平面BCD⊥平面ABC
(2)求证:AF//平面BDE
(3)求四面体B-CDE的体积
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设函数
(1)求函数
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知△ABC内角A、C、B成等差数列,A、B、C的对边分别为



正确答案
∵内角A、C、B成等差数列,A+C+B=

∵
由正弦定理
∵
解①②组成的方程组,得
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列

(1)证明:数列

(2)设
正确答案
证明:(1)由
当

即
∴

又
∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
20.我国发射的天宫一号飞行器需要建造隔热层.已知天宫一号建造的隔热层必须使用20年,每厘米厚的隔热层建造成本是3万元,天宫一号每年的能源消耗费用C(万元)与隔热层厚度

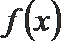
(1)求
(2)当隔热层修建多少厘米厚时,总费用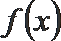
正确答案
(1)当
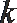
(2)
当且仅当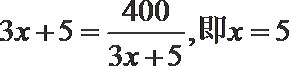
即隔热层修建5厘米厚时,总费用达到最小值,最小值为35万元.
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)若


(2)若


(3)在(1)的条件下,是否存在实数b,使得函数

正确答案
解:∵
∴
(1)依题意,
即
∴
得

∴
(2)∵
∴在


即
∴只需
而当
∴
(3)函数

即方程
∴
∴x=0是其中一个根,∴方程
∴
∴
∴存在满足条件的b值,b的取值范围是
解析
解析已在路上飞奔,马上就到!