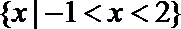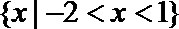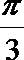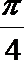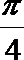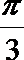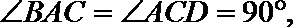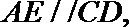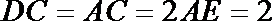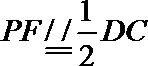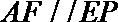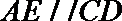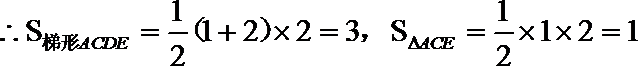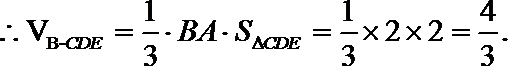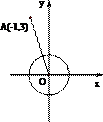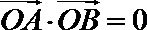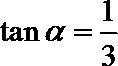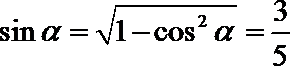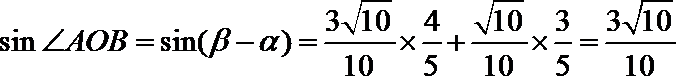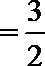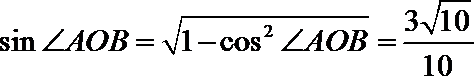- 真题试卷
- 模拟试卷
- 预测试卷
1. 设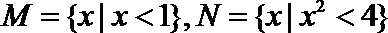
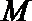

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 若不等式组

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知函数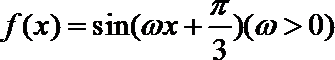
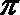
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 下列结论错误的是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若向量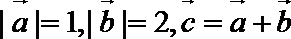
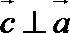

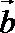
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知一个空间几何体的三视图如图所示,
根据图中标出的尺寸(单位:cm),可得这个
几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 若点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 若存在正数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 若关于



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
14. 用斜二测画法画一个边长为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.一种平面分形图的形成过程如下图所示,第一层是同一点出发的三条线段,长度均为1,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知





正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
20. 在△







(1)求
(2)设

正确答案
(1)由

因为


又因为 
(2)解法一:由正弦定理得
其中



解法二:由余弦定理得

又因为
解得
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知等差数列




(1)求

(2)令



正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
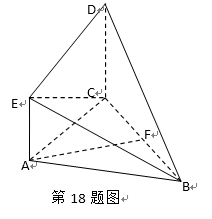
18.如图,直角梯形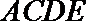
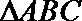

(1)求证:
(2)求四面体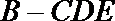
正确答案
(1)证:取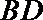

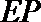

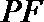
又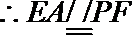
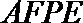
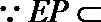
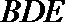
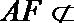
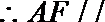
(2)解: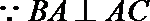

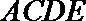


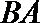

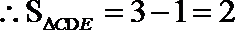
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数


(1)若曲线



(2)求函数
(3)当



正确答案
(1)由

又曲线





(2)
1当


2当





所以





综上,当





(3)当


即
则










所以


解析
解析已在路上飞奔,马上就到!
知识点
17. 在平面直角坐标系
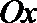
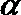


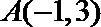
(Ⅰ)若

(Ⅱ)若


正确答案
(1)解法1:由题可知: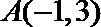
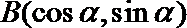


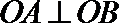
∴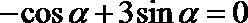
解法2:由题可知: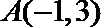



∵
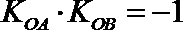

(2)解法1:由(1)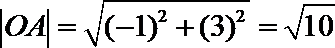
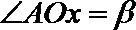
∴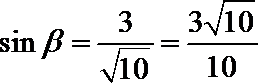
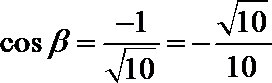

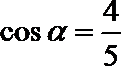
得
∴
解法2: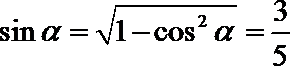
即: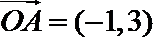



则
解析
解析已在路上飞奔,马上就到!
知识点
21. 国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费,每一年度申请总额不超过6000元。某大学2010届毕业生王某在本科期间共申请了


签约的单位提供的工资标准为第一年内每月







(Ⅰ)用



(Ⅱ)若王某恰好在第36个月(即毕业后三年)还清贷款,求
(Ⅲ)当

(参考数据:
正确答案
(Ⅰ)
(Ⅱ)依题意,从第13个月开始,每个月的还款额为



令

即要使在三年全部还清,第13个月起每个月必须比上一个月多还
(Ⅲ)设王某第
整理可得


即王某工作
这个月王某的还款额为

第32个月王某的工资为
因此,王某的剩余工资为
解析
解析已在路上飞奔,马上就到!