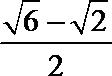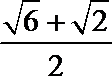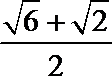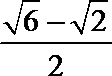- 真题试卷
- 模拟试卷
- 预测试卷
1.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.如果函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.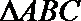
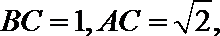
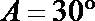
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知椭圆的一个焦点为F,若椭圆上存在点P,满足以椭圆短轴为直径的圆与线段PF相切于线段PF的中点,则该椭圆的离心率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设二元一次不等式组

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.三棱锥







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知点A(1,-1),点B(3,5),点P是直线
正确答案
(2,2)
解析
解析已在路上飞奔,马上就到!
知识点
12.已知直线


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
15.现有下列命题:
①命题“

②若



③函数

④若非零向量


其中正确命题的序号有__________。
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
16.已知在



(Ⅰ)求
(Ⅱ)若


正确答案
解: (Ⅰ)因为

∴
(Ⅱ)由

则
由正弦定理,得
∴
解析
解析已在路上飞奔,马上就到!
知识点
17.将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为a,第二次出现的点数为b.设复数
(1)求事件“
(2)求事件“
正确答案
解:(1)

∴b=3
又依题意,b可取1,2,3,4,5,6
故出现b=3的概率为
即事件“
(2)由已知,
可知,b的值只能取1、2、3
当b=1时, 
当b=2时, 
当b=3时, 
由上可知,共有9种情况下可使事件“
又a,b的取值情况共有36种,故事件“
解析
解析已在路上飞奔,马上就到!
知识点
18.在直三棱柱







(1)求证:

(2)求三棱锥
(3)试在



正确答案
(1)证明:
















即



(2)解:

=
(3)当


证明:连
设












解析
解析已在路上飞奔,马上就到!
知识点
20.已知



(1)求证: 数列
(2)设



正确答案
(Ⅰ)解:



(Ⅱ)


当

当


解析
解析已在路上飞奔,马上就到!
知识点
19

(1)试求f(x)的单调区间;
(2)求证:不等式

正确答案
(1)
当



当








综上所述,当


当



(2)证明:∵1<x<2,∴
令

由(1)知,当a=1时,
∴

∴
∴
∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
21.已知点


(Ⅰ)求点P的轨迹方程;
(Ⅱ)过点C的直线m与点P的轨迹交于两点




正确答案
解:(Ⅰ) 由已知

所以

平方整理得.
(Ⅱ)由题意可知设直线

设直线

由
若



由韦达定理可得
故直线

解析
解析已在路上飞奔,马上就到!