- 真题试卷
- 模拟试卷
- 预测试卷
4.已知命题


正确答案
解析
p是真命题,比如当x=100时满足条件,q是假命题,当x=0就不满足,故只有C答案正确。
考查方向
解题思路
p是真命题,比如当x=100时满足条件,q是假命题,当x=0就不满足。
易错点
全称命题和特称命题的判断出错。
知识点
6.已知双曲线


曲线的一条渐近线与抛物线的准线的交点坐标为
则双曲线的方程为
正确答案
解析
由已知可得

考查方向
解题思路
先画示意图,然后根据双曲线的一条渐近线与抛物线的
准线的交点坐标为
双曲线的方程。
易错点
不会转化为所学内容来做。
知识点
7.如图给出的是计算
正确答案
解析
首先应满足

考查方向
解题思路
根据已知来填写。
易错点
判断框出错。
知识点
8.函数
正确答案
解析
先判断出函数是一个奇函数,故排除B,C,然后当x=1时函数的值为0,
考查方向
解题思路
根据函数的奇偶性先排除一些答案,然后特殊点代入即可。
易错点
函数的图像不会判断。
知识点
1.集合

正确答案
解析
由

考查方向
解题思路
由已知先将两个集合都求出来再求并集。
易错点
粗心出错。
知识点
2.复数

正确答案
解析
由
考查方向
解题思路
先化简之后再来计算a的值。
易错点
对复数的概率模糊。
知识点
3.已知

正确答案
解析


考查方向
解题思路
先计算出向量的平方再开根号即可。
易错点
求模不会转化为先求向量的平方。
知识点
5.函数

正确答案
解析



考查方向
解题思路
先用降幂公式化简,再利用辅助角公式合二为一去做。
易错点
不会用公式化简。
知识点
9.已知数列




的前

正确答案
解析
由




考查方向
解题思路
先判断出该数列是一个等差数列,然后再求最值。
易错点
不会转化来做。
知识点
12.设直线








正确答案
解析
设
























考查方向
解题思路
点差法来解答。
易错点
计算失误。
知识点
10. 正四面体的四个面上分别写有数字1,2,3,4,把两个这样的四面体抛在桌面上,则露
在外面6个数字分别为3,1,2,4,1,4的概率为
正确答案
解析
只考虑没有露在外面的数字则共有

考查方向
解题思路
先算出基本事件的总数,在计算出题目要求的事件的个数,由公式即可算出。
易错点
计算失误。
知识点
11.如图,网格纸上小正方形的边长为
某几何体的三视图,则该几何体最长的棱长等于
正确答案
解析
该几何体为三棱锥,其棱长分别为:
知识点
13.各项为正数的等比数列




正确答案
解析
由




考查方向
解题思路
本题考查等比数列的性质及对数的运算法则。
易错点
不记得等比数列的性质。
知识点
15.已知直三棱柱



柱
正确答案
解析
设侧面
柱


考查方向
解题思路
根据题意先作出示意图,再来计算最小值。
易错点
不会转化。
知识点
16.已知函数

函数
正确答案
2
解析


















考查方向
解题思路
本题考查复合函数的零点及导数的应用。
易错点
不会计算。
知识点
14.设




正确答案
解析
求出M的最小值为-2,N的最大值为2,则
考查方向
解题思路
本题考查简单的线性规划问题分别计算出M,N的最小值和最大值即可。
易错点
最值点找错。
知识点
17.如图,在△




(1)若

(2)若

正确答案
【答案】(1)
解析
试题分析:本题属正余弦定理解三角形的问题,题目的难度是逐渐由易到难,(1)先由已知条件算出一个角的余弦值再利用余弦定理即可解出;(2)由余弦定理得到一个等式再利用基本不等式即可算出最值。
在△ADC中,AD=1,




(2)因为







考查方向
解题思路
本题考正余弦定理解三角形,解题步骤如下:(1)先由已知条件算出一个角的余弦值再利用余弦定理即可解出;(2)由余弦定理得到一个等式再利用基本不等式即可算出最值。
易错点
粗心计算失误。
知识点
18.为了解甲、乙两校高三年级学生某次期末联考地理成绩情况,从这
两学校中分别随机抽取30名高三年级的地理成绩(百分制)作为样本,样本数据的茎叶
图如图所示:
(1)若乙校高三年级每位学生被抽取的概率为0.15,求乙校高三年级学生总人数;
(2)根据茎叶图,分析甲、乙两校高三年级学生在这次联考中地理成绩(不要求计算);
(3)从样本中甲、乙两校高三年级学生地理成绩不及格(低于60分为不及格)的学生中随机抽取2人,求至少抽到一名乙校学生的概率.
正确答案
(1)
解析
试题分析:本题属茎叶图及古典概型的计算,(1)根据已知直接计算;(2)直接根据茎叶图来判断;(3)用列举法将所有基本事件一一列举出来,再将所求事件列举出来,最后利用古典概型的概率公式即可算出答案。
(1)因为每位同学被抽取的概率均为0.15,则高三年级学生总数
(3)由茎叶图可知,甲校有4位同学成绩不及格,分别记为:1、2、3、4;乙校有2位同
学成绩不及格,分别记为:5、6.则从两校不及格的同学中随机抽取两人有如下可能:(1,
2)、(13)、(1,4)、(1,5)、(1,6)、(2,3)、(2,4)、(2,5)、(2,6)、(3,4)、(3,5)、
(3,6)、(4,5)、(4,6)、(5,6),总共有15个基本事件.其中,乙校包含至少有一名学
生成绩不及格的事件为A,则A包含9个基本事件,如下:(1,5)、(1,6)、(2,5)、(2,
6)、(3,5)、(3,6)、(4,5)、(4,6)、(5,6).所以,
考查方向
解题思路
本题考查了茎叶图及古典概型的计算,解题步骤如下:(1)根据已知直接计算;(2)直接根据茎叶图来判断;(3)用列举法将所有基本事件一一列举出来,再将所求事件列举出来,最后利用古典概型的概率公式即可算出答案。
易错点
基本事件列举不全。
知识点
如图,在三棱柱





19.求证:

20.若异面直线


锥
正确答案
(1)见解析;
解析
试题分析:本题属立体几何证明和体积的计算,(1)利用线面平行的判定定理来证明;(2)利用等体积将要求的转化后再来求解。
1)取













考查方向
解题思路
本题考立体几何证明和体积的计算,解题步骤如下:(1)利用线面平行的判定定理来证明;(2)利用等体积将要求的转化后再来求解。
易错点
定理使用不完整,不会将体积转化来求。
正确答案
(2)
解析
试题分析:本题属立体几何证明和体积的计算,(1)利用线面平行的判定定理来证明;(2)利用等体积将要求的转化后再来求解。
(2)














考查方向
解题思路
本题考立体几何证明和体积的计算,解题步骤如下:(1)利用线面平行的判定定理来证明;(2)利用等体积将要求的转化后再来求解。
易错点
定理使用不完整,不会将体积转化来求。
已知椭圆


21.求椭圆
22.从椭圆








正确答案
(1)
解析
试题分析:本题属直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,(1)根据已经条件构造方程组;(2)先将
(1)


……4分
考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)根据已经条件构造方程组;(2)先将
易错点
计算不出来。
正确答案
(2)
解析
试题分析:本题属直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,(1)根据已经条件构造方程组;(2)先将
(2)设点














所以

考查方向
解题思路
本题考直线与圆锥曲线的位置关系,解题步骤如下:(1)根据已经条件构造方程组;(2)先将
易错点
计算不出来。
已知

23.若

24.设





正确答案
(1)极小值
解析
试题分析:本题属函数与导数,题目的难度是逐渐由易到难,(1)求导之后直接解出即可;(2)直接按照步骤来求。
(1)

时,











考查方向
解题思路
本题考函数与导数,解题步骤如下:(1)求导之后直接解出即可;(2)直接按照步骤来求。
易错点
计算量大,算不出来。
正确答案
(2)
解析
试题分析:本题属函数与导数,题目的难度是逐渐由易到难,(1)求导之后直接解出即可;(2)直接按照步骤来求。
(2)











































考查方向
解题思路
本题考函数与导数,解题步骤如下:(1)求导之后直接解出即可;(2)直接按照步骤来求。
易错点
计算量大,算不出来。
已知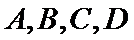
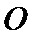
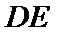
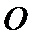


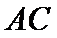
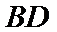
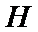
25.求证:
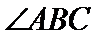
26.若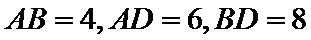
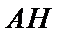
正确答案
【答案】(1)见解析;
解析
试题分析:本题属几何证明选讲中的证明和求线段长度的问题,(1)直接按照步骤来求;(2)利用三角形相似来证明。
(1)
又


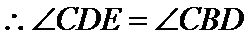

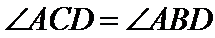
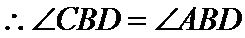
考查方向
解题思路
本题考几何证明选讲中的证明和求线段长度的问题,解题步骤如下:(1)直接按照步骤来求;(2)利用三角形相似来证明。
易错点
不会转化为所学知识来解答。
正确答案
【答案】(2)
解析
试题分析:本题属几何证明选讲中的证明和求线段长度的问题,(1)直接按照步骤来求;(2)利用三角形相似来证明。
(2)由(I)知
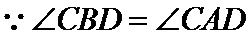
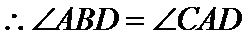


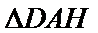
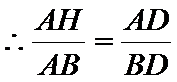
∵AB=4,AD=6,BD=8,∴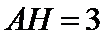
考查方向
解题思路
本题考几何证明选讲中的证明和求线段长度的问题,解题步骤如下:(1)直接按照步骤来求;(2)利用三角形相似来证明。
易错点
不会转化为所学知识来解答。















































































