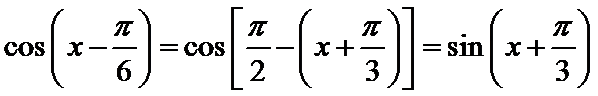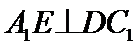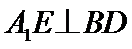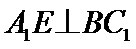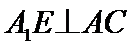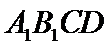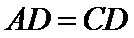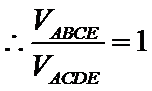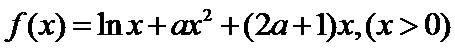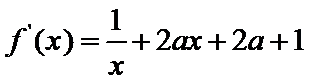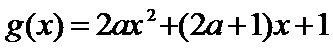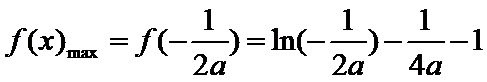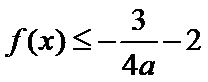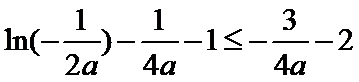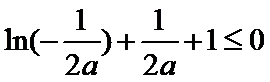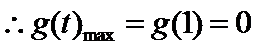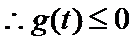- 真题试卷
- 模拟试卷
- 预测试卷
2.复平面内表示复数
正确答案
解析
由

考查方向
解题思路
直接利用复数代数形式的乘除运算化简复数z得答案
易错点
复数的乘除运算
1.已知集合


正确答案
解析
集合


考查方向
解题思路
由交集的定义直接求出元素
易错点
交集的定义与应用
3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是( )
正确答案
解析
由折线图可知,每年月接待游客量从8月份后存在下降趋势,故选A.
考查方向
解题思路
由折线图可知,很容易看出答案
易错点
折线图的运用
5.设


正确答案
解析
绘制不等式组表示的可行域,结合目标函数的几何意义可得函数在点



考查方向
解题思路
作出不等式组对应的平面区域,根据z的几何意义,利用数形结合即可得到结论.
易错点
z的几何意义
6.函数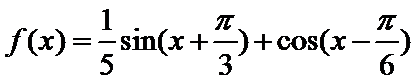
正确答案
解析
由诱导公式可得:
则: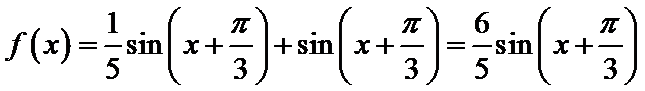
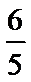
考查方向
解题思路
由诱导公式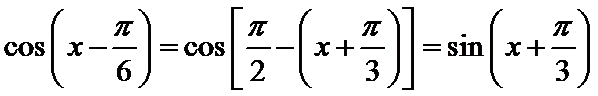
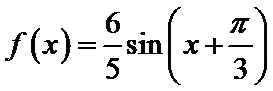
易错点
诱导公式的灵活运用
7.函数
正确答案
解析
当



考查方向
解题思路
当



易错点
灵活地运用数形结合解函数的图象
9.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
正确答案
解析
画出圆柱的轴截面



考查方向
解题思路
画出圆柱的轴截面,由题意直接求出
易错点
用轴截面解外接球
10.在正方体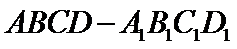
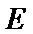
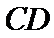
正确答案
解析
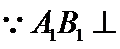
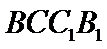
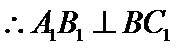
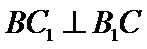
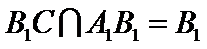
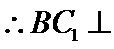
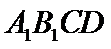
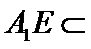
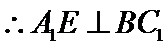
考查方向
解题思路
在正方体中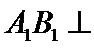
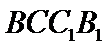
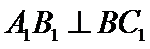
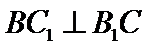
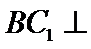
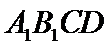
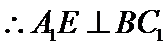
易错点
由线面垂直推出线线垂直
4.已知

正确答案
解析

考查方向
解题思路
由已知得
易错点

8.执行右面的程序框图,为使输出S的值小于91,则输入的正整数
正确答案
解析
若







考查方向
解题思路
通过程序框图的要求,写出每次循环的结果得到输出的值.
易错点
循环结构的条件判断
11.已知椭圆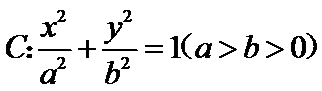
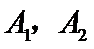
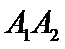
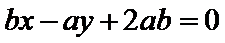
正确答案
解析
以线段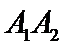
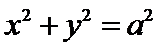
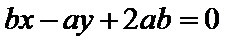
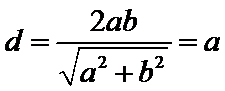
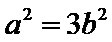
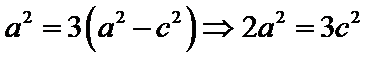
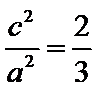
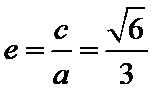
考查方向
解题思路
以线段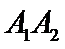
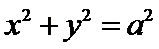
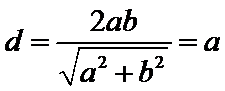
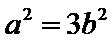
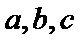
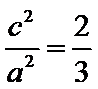
易错点
椭圆的几何性质
12.已知函数

正确答案
解析

得


则

考查方向
解题思路
求导


易错点
函数唯一的零点的转化
13.已知向量



正确答案
2
解析
由题意可得:
考查方向
解题思路
由向量垂直定义直接就可以求出结果
易错点
向量垂直的坐标运算
14.双曲线


正确答案
5
解析
由双曲线的标准方程可得渐近线方程为:

考查方向
解题思路
由题直接算出双曲线的渐近线方程为
易错点
双曲线的渐近线方程
15.




正确答案
解析
由题意:



考查方向
解题思路
由正弦定理直接算出


易错点
(1)在解三角形中正弦定理应用(2)大边对大角
16.设函数


正确答案
解析
由题意得: 当










考查方向
解题思路
由题意得,在


易错点
分段进行化简
18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶









以最高气温位于各区间的频率代替最高气温位于该区间的概率。








正确答案
(1)
解析
(1)需求量不超过300瓶,即最高气温不高于
∴所求概率为
(2)





不低于
∴

考查方向
解题思路
(1)需求量不超过300瓶,即最高气温不高于




易错点
转化与化归的思想的运用
20.(12分)在直角坐标系





(1) 能否出现
(2) 证明过

正确答案
(1)不能(2)见解析
解析
(1)令




假设



(2)令圆与

令圆的方程为
令得

令

点




考查方向
解题思路
(1)设










易错点
(1)二次方程韦达定理;(2)过三点的圆
17.(12分)设数列

(1)求
(2)求数列

正确答案
(1)
解析
(1)当
当


① -②得
即
验证
所以
(2)
考查方向
解题思路
(1)当




易错点
裂项相减法及计算能力
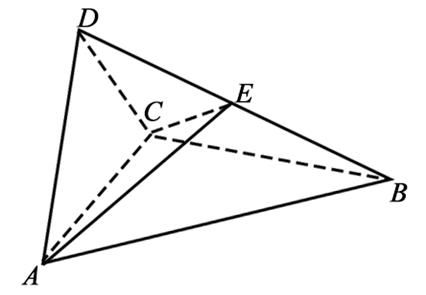
19.(12分)如图,四面体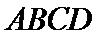
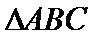
(1)证明: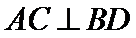
(2)已知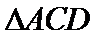

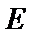
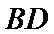
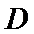
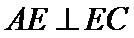
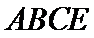
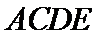
正确答案
(1)见解析 (2)1
解析
(1)证明:取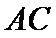
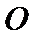
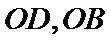
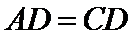
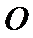
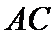
∴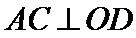
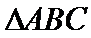
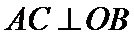
又∵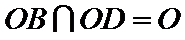
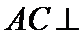
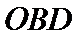
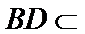
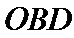
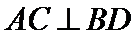
(2)由题意,令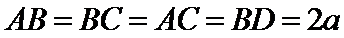
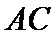
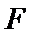
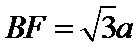
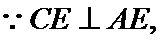
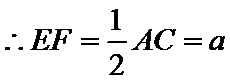
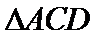
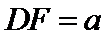
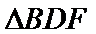
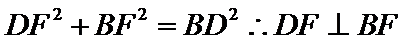
又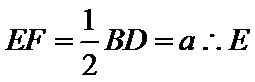
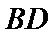
考查方向
解题思路
(1)由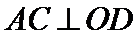
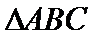
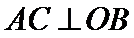
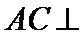
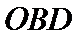
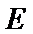
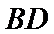
易错点
线面垂直的判定定理
21.(12分)设函数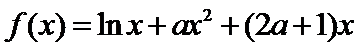
(1)讨论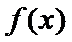
(2)当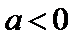
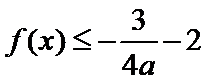
正确答案
(1)见解析(2)见解析
解析
(1)由
有
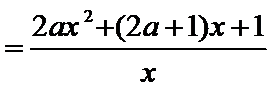
①当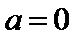
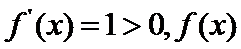
② 当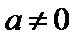
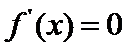
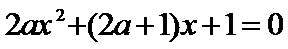
解得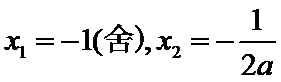
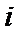
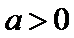
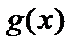
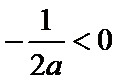
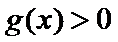
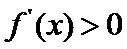
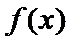
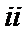
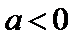
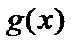
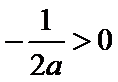
此时,在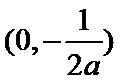
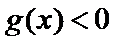
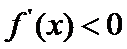
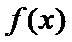
在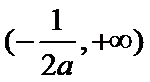
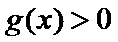
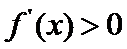
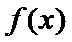
(2)由(1)可得:
故要证
即证
即证
即证
令
则
令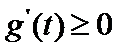
考查方向
解题思路
(1)对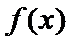
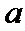
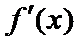
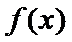
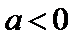
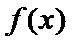
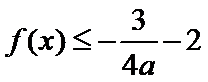
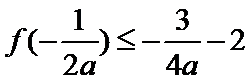
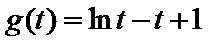
易错点
(1)导数在研究函数中的应用; (2)构造函数
22.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
选修4―4:坐标系与参数方程](10分)
在直角坐标系












(1) 写出
(2) 以坐标原点为极点,





正确答案
(1)
解析
(1)直线的普通方程为
消去


(2)化为普通方程为
联立
∴

考查方向
解题思路
(1)由两个参数方程分别消去



23.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
选修4—5:不等式选讲](10分)
已知函数
(1)求不等式
(2)若不等式

正确答案
(1)
解析
⑴


①当
②当


③当



(2)原式等价于存在
成立,即
设
由(1)知
当
其开口向下,对称轴
∴
当
其开口向下,对称轴为
∴
当
其开口向下,对称轴为
∴
综上
∴

考查方向
解题思路
(1)对


易错点
(1)分段讨论(2)恒成立问题