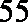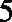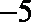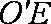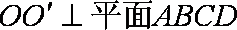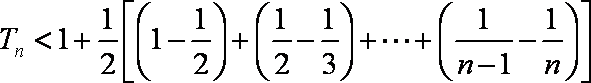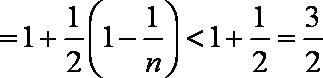- 真题试卷
- 模拟试卷
- 预测试卷
1.设全集为R, 函数

正确答案
解析
略。
知识点
4.交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查。假设四个社区驾驶员的总人数为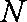
正确答案
解析
略。
知识点
5.已知直线



正确答案
解析
略。
知识点
8.设△ABC的内角A, B, C所对的边分别为a, b, c, 若
形状为( )
正确答案
解析
略。
知识点
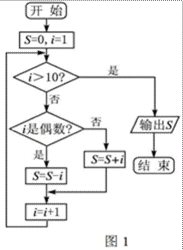
6.阅读如图1的程序框,则判断运行结果为 ( )
正确答案
解析
略。
知识点
10.若定义在区间








正确答案
解析
略。
知识点
2.复数
正确答案
解析
略。
知识点
3.已知向量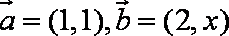
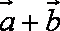

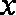
正确答案
解析
略。
知识点
7.如果点P在平面区域

最小值为( )
正确答案
解析
略。
知识点
9.已知





正确答案
解析
略。
知识点
11.已知数列



正确答案
26
解析
略。
知识点
12.已知某运动物体的位移



正确答案
3e
解析
略。
知识点
13.某三棱锥的三视图如右图所示,则该三棱锥的最长棱的棱长为 。
正确答案
解析
略。
知识点
15.已知




正确答案
解析
略。
知识点
14.已知曲线C1与C2的极坐标方程分别为 


正确答案
解析
略。
知识点
16.已知函数


(1)求函数
(2)若函数





正确答案
见解析。
解析
解法一:(1)因为



所以



因为

所以

(2)由(1)知

因为

要使函数



因此实数

解法二:(1)同解法一。
(3)由(1)知

令

因此函数

令

因此函数

要使函数

只有


知识点
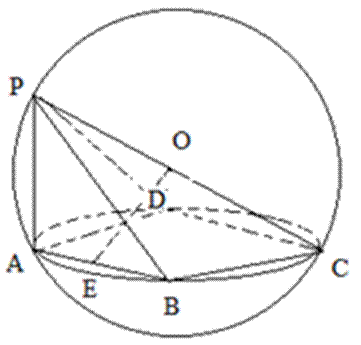
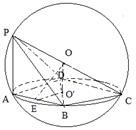
18.已知点P,A,B,C,D是球O表面上的点,且球心O在线段PC上,PA⊥平面ABCD,E为AB的中点,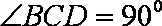
(1)求证:OE//平面PAD;
(2)若PA=4, AB=4, AD=3,求三棱锥O—ADE的体积。
正确答案
见解析。
解析
(1)设BD的中点为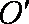
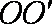
则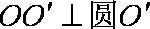
所以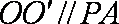
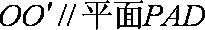
又因为E为AB的中点
所以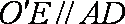
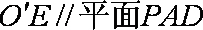
又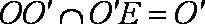
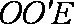
又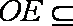
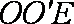
(2)因为E为AB中点,所以AE=
因为点P,C在球面上,O为球心,所以PC为球的直径,O为PC的中点,
所以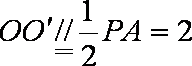
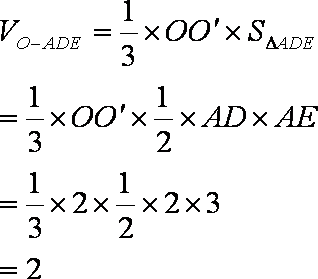
知识点
19.已知数列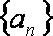
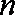
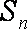
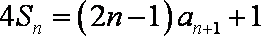
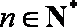
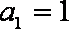
(1)求证:数列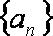
(2)设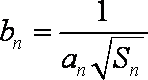
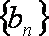
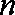
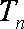
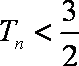
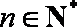
正确答案
见解析。
解析
(1)由题设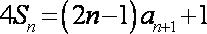
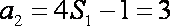
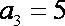
当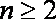
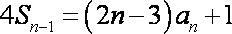
两式相减得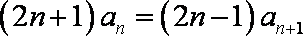
方法一:由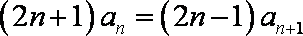
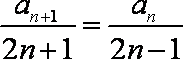

则数列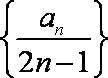
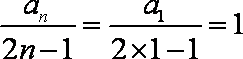
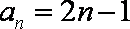
所以数列
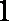
方法二:由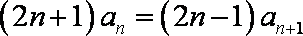
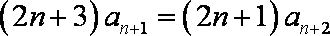
两式相减得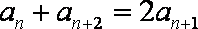
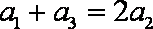
所以数列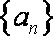
(2)由(Ⅰ)得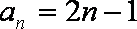
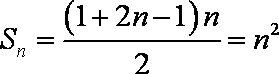
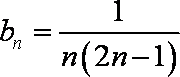
当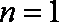
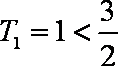
当
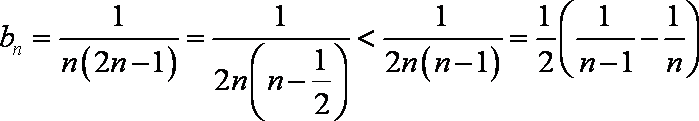
所以
综上所述,命题得证。
知识点
17.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
⑴ 从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
⑵ 在本次训练中,从两班中分别任选一个同学,比较两人的投中次数,求甲班同学投中次数高于乙班同学投中次数的概率。
正确答案
见解析。
解析
(1)两个班数据的平均值都为7,
甲班的方差
乙班的方差
因为
(2)甲班1到5号记作



将“甲班同学投中次数高于乙班同学投中次数”记作
则

所以甲班同学投中次数高于乙班同学投中次数的概率为
知识点
20.如图,在平面直角坐标系














(1)求抛物线的标准方程;
(2)求证:
(3)若直线


正确答案
见解析。
解析
(1)设抛物线的方程为

所以抛物线的方程为:




由


所以切线AC的方程为:
整理得:
且C点的坐标为
同理得切线BD的方程为:
且D点的坐标为
由(1)(2)消去y,得
又直线AD的方程为:
直线BC的方程为:
由(3)(4)消去y,得


(3)由题意,设

所以
所以直线AB的方程为