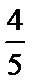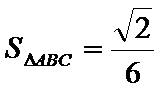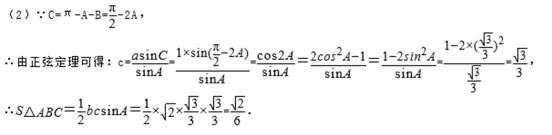- 真题试卷
- 模拟试卷
- 预测试卷
4.已知向量




正确答案
解析
考查方向
解题思路
利用向量的坐标运算求出两个向量的坐标;利用向量共线的充要条件列出方程求出m的值。
易错点
共线与垂直的条件,出现混淆。
知识点
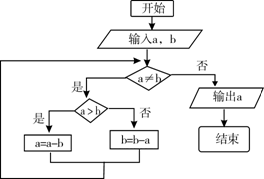
8.下边程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”,执行该程序框图,若输入的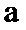
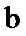
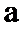
正确答案
解析
由a=14,b=18,a<b,
则b变为18-14=4,
由a>b,则a变为14-4=10,
由a>b,则a变为10-4=6,
由a>b,则a变为6-4=2,
由b>a,则b变为4-2=2,
由a=b=2,
则输出的a=2.
故选:B.
考查方向
解题思路
由循环结构的特点,先判断,再执行,分别计算出当前的a,b的值,即可得到结论
易错点
分支的方向出现问题。
知识点
9.已知等比数列



正确答案
解析
解:设等比数列{an}的公比是q,因为


考查方向
解题思路
设等比数列{an}的公比是q,根据题意和等比数列的通项公式列出方程,化简后求出q的值,即可求出a2
易错点
计算错误,主要是用换元法。
知识点
10.已知双曲线


正确答案
解析
解:由题意可得 F2(

20=PF12+PF22﹣2PF1•PF2cos60°=(PF1﹣PF2)2+PF1•PF2=16+PF1•PF2,
∴PF1•PF2=4.
S△F1PF2=



考查方向
解题思路
由余弦定理可得 PF1•PF2=4,再根据面积公式即可得到。
易错点
和椭圆的概念混淆。
知识点
1.已知集合A=


正确答案
解析
利用并集运算为A。
考查方向
解题思路
运用集合的运算性质。
易错点
集合A的补集和并集的符号。
知识点
2.已知复数Z=


正确答案
解析
考查方向
解题思路
利用复数代数形式的乘除运算,可求得z,利用z为纯虚数即可求得答案.
易错点
纯虚数与实数易混淆。
知识点
3.已知变量






正确答案
解析
解题思路
易错点
出现计算上的错误,再就是不知道过样本中心点。
知识点
5. 设




正确答案
解析
由等差中项性质得:
考查方向
解题思路
利用等差中项的概念,可以得到第三项,再利用前五项的和与第三项的关系可得。
易错点
利用前n项和公式,找不到前五项和和已知条件的关系。
知识点
6.某四面体的三视图均为直角三角形,如图所示,则该四面体的表面积为( )
正确答案
解析
将三视图还原为直方图如图所示,
这时底面积为


考查方向
解题思路
将三视图还原为直方图如图所示,利用已知条件可求得。
易错点
还原直观图出现问题。
知识点
7.已知三点A(1,0),B(0,


正确答案
解析
考查方向
解题思路
利用外接圆的性质,求出圆心坐标,再根据圆心到原点的距离公式即可求出结论.
易错点
求圆心时候出现运算问题。
知识点
11.已知





正确答案
解析
利用奇偶性作出函数的图像,观察得答案为A,
考查方向
解题思路
利用函数的图像观察出答案。
易错点
在解题时,主要出现了每一段的限制。
知识点
12.已知函数





正确答案
解析
构造函数







考查方向
解题思路
根据条件构造函数
易错点
构建函数时候构建错误函数。
知识点
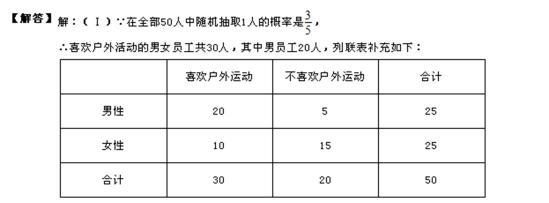
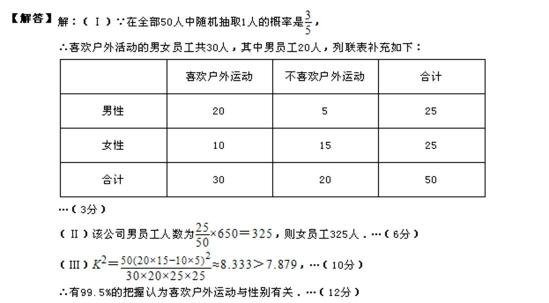
为了提高全民的身体素质,某地区增加了许多的户外运动设施为本地户外运动提供服务,为了进一步了解人们对户外运动的喜爱与否,随机对50人进行了问卷调查,已知在这50人中随机抽取1人抽到喜欢户外运动的概率为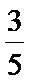
19.请将上面的列联表补充完整;
20.是否有99.5%的把握认为“喜欢户外运动与性别有关”?并说明你的理由;
21.根据分层抽样的方法从喜欢户外运动的人中抽取6人作为样本,从6人中随机抽取三人进行跟踪调查,那么这三人中至少有一名女性的概率是多少?
下面的临界值表仅供参考:
(参考公式: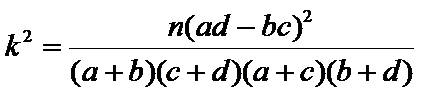
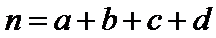
正确答案
见解析
解析
考查方向
解题思路
易错点
分层时候计算问题。再就是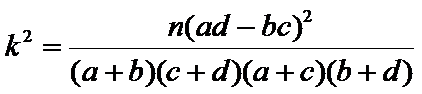
正确答案
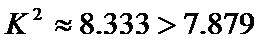
解析
考查方向
解题思路
易错点
分层时候计算问题。再就是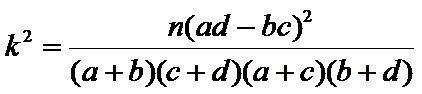
正确答案
解析
从六人中选出三人的方法数为n=20.其中三人中至少有一名女性的事件与没有女生的事件是对立事件,没有女生的基本事件数为4,所以概率为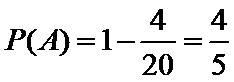
考查方向
解题思路
易错点
分层时候计算问题。再就是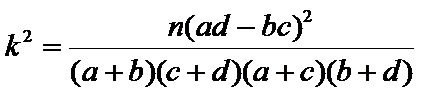
已知椭圆



24.求抛物线
25.设










正确答案
抛物线
解析
由题意:抛物线C2:x2=2py的焦点为(0,p/2),椭圆的焦点为(±



考查方向
解题思路
由焦点坐标和距离公式即可得到p;
易错点
容易出现计算错误。
正确答案
m的取值范围是(0,
解析
联立椭圆方程和抛物线方程,解得A(2,1),由题意得直线AB的方程为y﹣1=k(x﹣2),联立椭圆方程消去y,得(2k2+1)x2+4k(1﹣2k)x+2(1﹣2k)2﹣6=0,则xAxB=

















考查方向
解题思路
设出直线AB的方程,联立椭圆方程,运用韦达定理和弦长公式,求得|AB|,再设直线AC的方程,联立抛物线方程,运用韦达定理和弦长公式,可得|AC|,再求m的范围,即可得到.
易错点
容易出现计算错误。
在
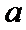
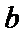
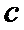
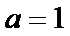
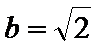
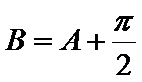
17.求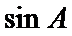
18.求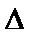
正确答案
解析
考查方向
解题思路
由已知可得A为锐角,由正弦定理,两边平方整理可解得sinA的值.
易错点
诱导公式的符号问题。
正确答案
解析
考查方向
解题思路
利用三角形内角和定理可求C,由正弦定理可得c,根据三角形面积公式即可得解.
易错点
诱导公式的符号问题。
如图,三棱柱ABC—A1B1C1 的侧棱AA1

22.求证:CF//平面AB1E;
23.求点C到平面AB1E的距离。
正确答案
见解析
解析
证明:取AB中点M,连MF,ME,∵E为CC1中点,F为AB中点,∴MF∥B1B,MF=1/2B1B,EC∥B1B,EC=1/2B1B,∴MF∥EC,且MF=EC,∴MFCE为平行四边形,∴CF∥EM,∵CF⊄平面AB1E,EM⊂平面AB1E,∴CF∥平面AB1E.
考查方向
解题思路
取AB中点M,连MF,ME,易证四边形MFCE是平行四边形,利用线面平行的判定定理即可证得CF∥平面AB1E;
易错点
本题易错点是∵CF⊄平面AB1E,EM⊂平面AB1E。
正确答案
点C到平面AB1E的距离为
解析
解:∵AA1⊥底面ABC,∴侧面AC1⊥底面ABC,又∠ACB=90°,BC垂直于交线AC,∴BC⊥侧面AC1.∵AC=BC=1,AA1=2,∴S△ACE=


考查方向
解题思路
依题意,可证得BC⊥侧面AC1,利用等体积转换,即可求出三棱锥C-AB1E的体积.进而求高。
易错点
本题易错点是∵CF⊄平面AB1E,EM⊂平面AB1E。
已知函数
26.若


27.求

正确答案
见解析
解析
依题意:f′(x)=




考查方向
解题思路
由于f(1)=﹣

易错点
恒成立和存在性问题的区别。
正确答案
实数a的取值范围是(﹣∞,﹣
解析
由f(x)=alnx+





考查方向
解题思路
由于f(1)=﹣

易错点
恒成立和存在性问题的区别。
设函数



28.求
29.若不等式

正确答案
函数
解析
解:f(x)=2|x-2|-x+5=


考查方向
解题思路
确定函数f(x)在区间(-∞,2)上单调递减,在区间[2,+∞)上单调递增,可得函数f(x)=2|x-2|-x+5的最小值
易错点
三角形不等式的符合问题。
正确答案

解析
解:f(x)=2|x-2|-x+5=


考查方向
解题思路
确定函数f(x)在区间(-∞,2)上单调递减,在区间[2,+∞)上单调递增,可得函数f(x)=2|x-2|-x+5的最小值
易错点
三角形不等式的符合问题。
13.若



正确答案

解析
做可行域

考查方向
解题思路
做可行域(如图)作然后作目标函数的直线,平移得到最优解。
易错点
容易出现最优解的错误。
知识点
14.已知双曲线过点(4,

正确答案
解析
考查方向
解题思路
易错点
容易出现渐近线的斜率k=a/b.
知识点
15.已知曲线


正确答案

解析
考查方向
解题思路
求出y=x+lnx的导数,求得切线的斜率,可得切线方程,再由于切线与曲线y=ax2+(a+2)x+1相切,有且只有一切点,进而可联立切线与曲线方程,根据△=0得到a的值.
易错点
有一个切点,满足切线方程,容易出现多根情况。
知识点
16.设





正确答案
解析
考查方向
解题思路
通过an+1=Sn+1-Sn=SnSn+1,并变形可得数列
易错点
公差和首项出现问题。