文科数学 2010年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．在等比数列中，已知，那么（）

A16

B12

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：单选题

分值: 5分

4．若，且，则（）

C或

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：单选题

分值: 5分

5．设等比数列的前项和为，已知，且(n∈N*)，则（）

A200

C－2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

7．一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积是那么这个三棱柱的体积是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：单选题

分值: 5分

10．已知全集R，集合,若a>b>0，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

1．已知，且，则的值等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

同角三角函数间的基本关系

题型：单选题

分值: 5分

8.在平面向量中有如下定理：设点O，P，Q，R为同一平面内的点，则P、Q、R三点共线的充要条件是：存在实数t，使．如图，在ΔABC中，点E为AB边的中点，点F在AC边上，且CF＝2FA，BF交CE于点M，设，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

9．在平面直角坐标系中，O为坐标原点，设向量，其中。若，且，C点所有可能的位置区域用阴影表示正确的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

6．设曲线在点处的切线与直线垂直，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数研究函数的单调性

题型：单选题

分值: 5分

3．设为平面，为直线，则的一个充分条件为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

12．已知方程表示的曲线是焦点在y轴上且离心率为的椭圆，则m＝___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

11．设复数，若z为纯虚数，则实数m＝______。

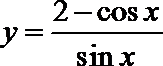
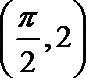
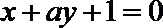
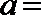
正确答案

－1

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

15．设等差数列的前项和为，已知，，则等差数列的公差d＝___________；___________。

正确答案

2；-2010

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

14.给出下列四个结论：

①函数在其定义域内是增函数；

②函数的图象关于直线对称；

③函数的最小正周期是2π；

④函数是偶函数．

其中正确结论的序号是___________。

正确答案

②④

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 5分

13．将函数与y＝3的图象所围成的封闭图形绕x轴旋转一周，则所得旋转体的表面积为___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

18.如图，三棱柱的底面是边长为a的正三角形，侧面是菱形且垂直于底面，＝60°，M是的中点．

（1）求证：BMAC；

（2）求三棱锥的体积．

正确答案

（1）略（2）

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：简答题

分值: 12分

17．国家教育部、体育总局和共青团中央曾共同号召，在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动．为此某网站于2010年1月18日至24日，在全国范围内进行了持续一周的在线调查，随机抽取其中200名大中小学生的调查情况，就每天的睡眠时间分组整理如下表所示：

（Ⅰ）估计每天睡眠时间小于8小时的学生所占的百分比约是多少；

（Ⅱ）该网站利用上边的算法流程图，对样本数据作进一步统计

正确答案

解：（Ⅰ）由样本数据可知，每天睡眠时间小于8小时的频率是

．

由此估计每天睡眠时间小于8小时的学生约占88%．

（Ⅱ）输入的值后，由赋值语句可知，

流程图进入一个求和状态．

设，数列的前项和为，则

．

故输出的S值为6．7．

S的统计意义是指被调查者每天的平均睡眠时间估计为6．7小时．

解析

解析已在路上飞奔，马上就到！

知识点

分布的意义和作用频率分布表程序框图

题型：简答题

分值: 12分

16.已知锐角△ABC的三内角A、B、C的对边分别是a，b，c，且。

（1）求角A的大小；

（2）求的值。

正确答案

解：（1）由已知条件及余弦定理得

∴．∵

（2）

= sin70=2sin70=－=－1

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 13分

20．已知定义在R上的函数(a，b，c，d为实常数)的图象关于原点对称，且当x＝1时f(x)取得极值．

（Ⅰ）求函数f(x)的解析式；

（Ⅱ）证明：对任意∈[－1，1]，不等式成立；

（Ⅲ）若函数在区间(1，∞)内无零点，求实数m的取值范围．

正确答案

解：（Ⅰ）因为f(x)的图象关于原点对称，则f(x)为奇函数，所以f(0)＝0，即d＝0．

又，即，则b＝0．

所以，．

因为当x＝1时f(x)取得极值，则，且．

即，故．

（Ⅱ）因为，则当－1≤x≤1时，．

所以f(x)在[－1，1]上是减函数．

所以当x∈[－1，1]时，，．

故当∈[－1，1]时，．

（Ⅲ）因为，则，

由，得，即，即．

所以在区间上是增函数，在上是减函数

从而在处取极小值．

又，若函数在区间(1，∞)内无零点，则

所以，即m≤1．

故实数m的取值范围是(－∞，1]．

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 13分

21．设数列为等比数列，数列满足，，已知，，其中．

（1）求数列的首项和公比；

（2）当时，求；

（3）设为数列的前项和，若对于任意的正整数，都有，求实数的取值范围．

正确答案

解：（1）由已知，所以，

，所以，

解得，所以数列的公比．

（2）当时，，

……………①，

……………②，

②①得，

所以，

．

（3），

因为，所以，由得，

注意到，当为奇数时

当为偶数时，

所以最大值为，最小值为．

对于任意的正整数都有，

所以，．

即所求实数的取值范围是．

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法

题型：简答题

分值: 13分

19．已知动点P到直线的距离比它到点F的距离大．

（Ⅰ）求动点P的轨迹方程；

（Ⅱ）若点P的轨迹上不存在两点关于直线l：对称，求实数的取值范围．

正确答案

解：（Ⅰ）据题意可知，点P到直线的距离等于它到点F的距离

所以点P的轨迹是以点F为交点，直线为准线的抛物线．

因为，抛物线开口向上，故点P的轨迹方程是．

（Ⅱ）若，则直线l为x轴，此时抛物线与直线l相切．

若，设与直线l垂直的直线为，代入，得

设直线与抛物线的交点为，则，

从而．

假设点A，B关于直线对称，则AB的中点在l上，

所以，即．

由于方程(*)有两个不相等的实根，则．

所以

整理得，即．

由恒成立，所以，即．

所以当时，抛物线上存在两点关于直线对称．

故当抛物线上不存在两点关于直线l：对称时

实数的取值范围是．

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷