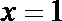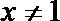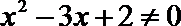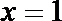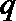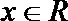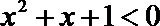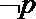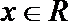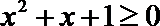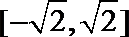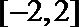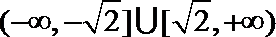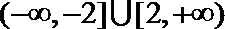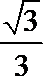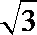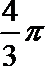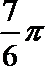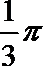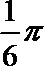- 真题试卷
- 模拟试卷
- 预测试卷
2.某连队身高符合建国60周年国庆阅兵标准的士兵共有45人,其中18岁~19岁的士兵有15人,20岁~22岁的士兵有20人,23岁以上的士兵有10人,若该连队有9个参加阅后的名额,如果按年龄分层选派士兵,那么,该连队年龄在23岁以上的士兵参加阅兵的人数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下列说法错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.对于平面

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.将4个相同的白球和5个相同的黑球全部放入3个不同的盒子中,每个盒子既要有白球,又要有黑球,且每个盒子中球数不能少于2个,则所有不同的放法的种数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.过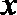
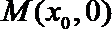
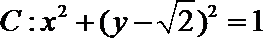
若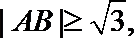
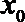
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知等差数列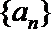
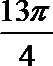
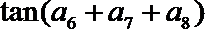
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知棱长为3的正方体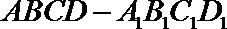
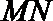
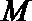
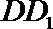
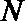
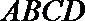
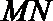
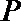
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.给出以下几个命题,正确的是__________.
①函数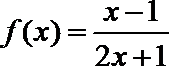
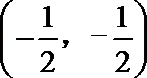
②已知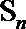
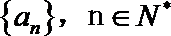
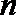
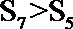
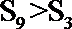
③函数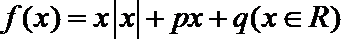
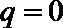
④已知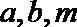
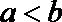
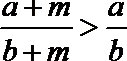
正确答案
②③④
解析
解析已在路上飞奔,马上就到!
知识点
14.若点



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.下图(右)实线围成的部分是长方体(左)的平面展开图,其中四边形ABCD是边长为

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知向量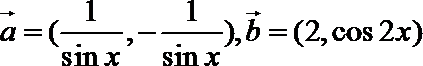
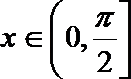
(1)试判断向量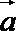
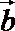
(2)求函数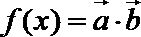
正确答案
(1)若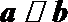
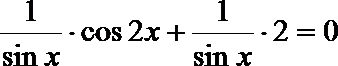
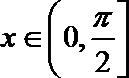
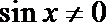
∴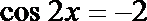
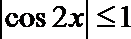
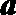
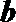
(2)∵
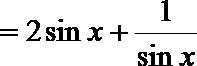
∵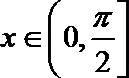
∴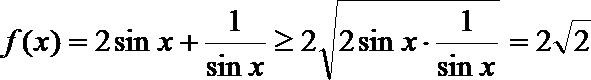
当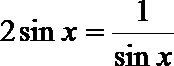
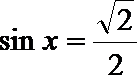
故函数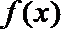
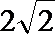
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知动圆


(1)求动圆
(2)设直线






正确答案
(1)圆



∵


设动圆




即
∴圆心





∴所求动圆

(2)由

设

△
由


设

△
∵


∴


解得

当

∵





当

∵

∴满足条件的直线共有9条.
解析
解析已在路上飞奔,马上就到!
知识点
18. 为预防
已知在全体样本中随机抽取1个,抽到B组疫苗有效的概率是0.33.
(1)求
(2)现用分层抽样的方法在全体样本中抽取360个测试结果,问应在C组抽取多少个?
(3)已知
正确答案
(1)
即

(2)C组样本个数为y+z=2000-(673+77+660+90)=500,
现
(3)设测试不能通过事件为A ,C组疫苗有效与无效的可能的情况记为(y,z) 由(2)知 

(465,35)、(466,34)、(467,33)、……(475,25)共11个
若测试不能通过,则77+90+z>200,即z>33
事件A包含的基本事件有:((465,35)、(466,34)共2个


解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数
(1)当

(2)试讨论函数
正确答案
(1)当
∴
(2) 当

当




则
当




则
当



当




则
综上所述:当



解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列




(1)求证:数列
(2)若数列




正确答案
略。
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,在直三棱柱ABC-A1B1C1中,
(1)求异面直线AE与A1C所成的角;
(2)若G为C1C上一点,且EG⊥A1C,试确定点G的位置;
(3)在(2)的条件下,求二面角A1-AG-E的大小
正确答案
(1)取B1C1的中点E1,连A1E1,E1C,则AE∥A1E1,
∴∠E1A1C是异面直线A
与A1C所成的角。设


所以异面直线AE与A1C所成的角为
(2).由(1)知,A1E1⊥B1C1,
又因为三棱柱ABC-A1B1C1是直三棱柱








所以G是CC1的中点
(3)连结AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,则EP⊥AC.
又

而PQ⊥AG 

由EP=a,AP=a,PQ=
所以二面角C-AG-E的平面角是


解析
解析已在路上飞奔,马上就到!