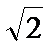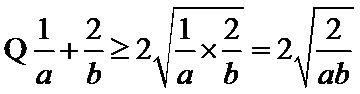- 真题试卷
- 模拟试卷
- 预测试卷
1.已知
正确答案
解析
由题意得,
考查方向
解题思路
直接根据复数的运算法则求解既可。
易错点
在计算上失误丢分。
知识点
2.在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图1所示
图1
若将运动员按成绩由好到差编为1-35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是
正确答案
解析
由茎叶图可知,在区间


考查方向
解题思路
先确定区间

易错点
不明白系统抽样的抽样过程导致出错。
知识点
3.设


正确答案
解析





考查方向
解题思路
先解不等式得到前后范围相同,后即可得到答案。
易错点
不会解不等式
知识点
6.若双曲线
正确答案
解析
由题意得


考查方向
解题思路
直接根据题意得到a,b,c之间的关系即可得到答案。
易错点
弄错渐近线方程导致结果出错。
知识点
7.若实数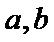
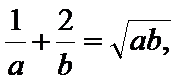
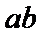
正确答案
解析
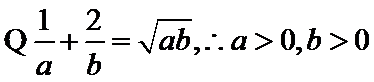

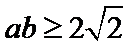
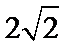
考查方向
解题思路
根据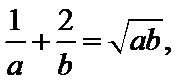
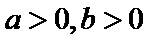
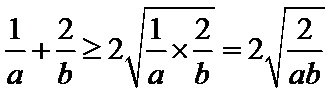
易错点
不会利用基本不等式得到
知识点
8.设函数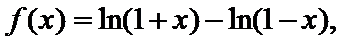
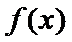
正确答案
解析
显然,f(x)的定义域为(-1,1),关于原点对称,又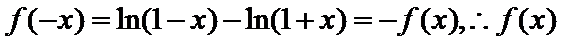
考查方向
解题思路
分求函数的定义域后发现其关于原点对称,后利用奇偶性的定义得到其为奇函数,最后利用奇函数在对称的区间上单调性相同,得到其单调性。
易错点
对于函数的性质不理解导致出错。
知识点
4.若变量


正确答案
解析
画出可行域如图三角形所示,由图可知,最优解为A,易知点A(0,1),所以
考查方向
解题思路
先画出可行域,然后将目标函数平移即可得到答案。
易错点
可行域画错导致结果出错。
知识点
5.执行如图1所示的程序框图,如果输入

正确答案
考查方向
易错点
1. 不清楚循环结束的条件导致出错;
知识点
9.已知点A,B,C在圆


最大值为
正确答案
解析
由题意得,AC为圆的直径,故可设






考查方向
解题思路
先由题意得到AC为圆的直径,后设出所需要点的坐标后把所求的结果表示成函数的形式后求其最值即可。
易错点
1.不会转化题中的条件
知识点
10.

正确答案
解析
分析题意可知,问题等价于圆锥的内接长方体的体积的最大值,设长方体体的长、宽、高分别为x 、y、h,长方体上底面截圆锥的截面半径为a,则x2+y2=(2a)2=4a2,如下图所示,则可以



考查方向
解题思路
1.先根据三视图得到原来的几何体为圆锥,后得到x2+y2=(2a)2=4a2,2.然后将长方体的体积表示为关于a的函数后利用基本不等式求最值即可。
易错点
1.找不到题中给出的关系式 x2+y2=(2a)2=4a2;2.不会利用基本不等式求最值。
知识点
12.在直角坐标系


正确答案
解析
由极坐标方程得


考查方向
解题思路
先将极坐标方程两边同乘以
易错点
极坐标和直角坐标的互化公式记不住出错。
知识点
11.已知集合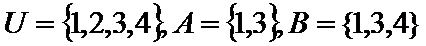
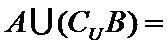
正确答案
{1,2,3}
解析
由题意得,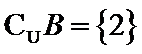
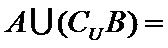
考查方向
解题思路
先求出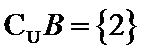
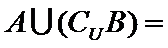
易错点
马虎出错。
知识点
14.若函数
正确答案
(-2,+∞)
考查方向
易错点
1.不注意指数函数的有界性导致出错;
知识点
15.已知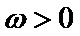
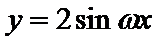
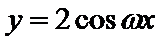
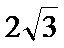
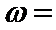
正确答案
解析
由题根据三角函数图像和性质可得交点坐标为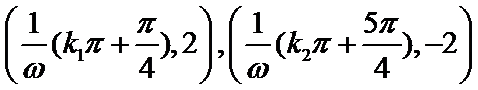
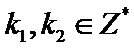
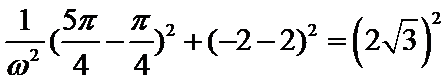
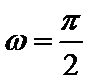
考查方向
解题思路
由题奋进三角函数的周期性求得两个函数的交点坐标,根据距离最短的两个交点一定在同一个周期,结合勾股定理不难得到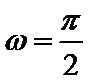
易错点
不能理解题中给出的条件导致没有办法入手解决。
知识点
13.若直线




正确答案
2
解析
由




考查方向
解题思路
先求出圆心到直线的距离后利用点到直线的距离公式即可。
易错点
不知道题中给出的120度如何转换导致出错。
知识点
某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是,从装有2个红球


16.用球的标号列出所有可能的摸出结果;
17.有人认为:两个箱子中中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由。
正确答案
所有可能的摸出结果为
解析
见答案
考查方向
本题主要考察古典概型的概率求法,意在考察考生的逻辑推理能力。
解题思路
先列举出所有可能的结果后利用古典概型的概率公式求解即可。
易错点
所有可能的摸出结果多列或少列导致出错;
正确答案
不正确,理由如下:
由(1)知,所以可能的摸出结果有12种,其中摸出的2个球都是红球的结果为


解析
不正确,理由如下:
由(1)知,所以可能的摸出结果有12种,其中摸出的2个球都是红球的结果为


考查方向
解题思路
先列举出所有可能的结果后利用古典概型的概率公式求解即可。
易错点
所有可能的摸出结果多列或少列导致出错;
如图4,直三棱柱ABC-A



20.证明:平面AEF⊥平面B

21.若直线A



正确答案
如图,因为三棱柱
所以




所以
解析
见答案
考查方向
解题思路
先证明



易错点
不会证明

正确答案

解析
设AB的中点为D,连接









由题设知,
所以,
在


故三棱锥F-AEC的体积
考查方向
解题思路
设AB的中点为D,证明


由题设知,
易错点
找不到直线与平面所成的角;
设数列{





22.证明:
23.求S
正确答案
(1)由条件,对任意

因而对任意

两式相减,得

又

故对一切

解析
见答案
考查方向
解题思路
当

两式相减,得


易错点
不说明当n=1的情况导致丢分;
正确答案
解析
由(1)知,




于是

综上所述,
考查方向
解题思路
通过求数列的奇数项和偶数项的和即可得到其对应的前n项和的通项公式。
易错点
不会分类求和,或不知道该如何求和。
设△ABC的内角A,B,C的对边分别为

18.证明:
19.若
正确答案
由


解析
见答案
考查方向
解题思路
由题及正弦定理得

易错点
不会想到切割化弦;
正确答案



解析
因为
由(1)知


故



综上所述,


考查方向
解题思路
由两角和与差的公式化简得


易错点
做第(2)问时联系不上第(1)问的结论。
已知抛物线C











24.求C
25.若|AC|=|

正确答案
解析
由


所以 















考查方向
解题思路
根据已知条件可求得


易错点
不会转化题中给出的条件

正确答案

考查方向
易错点
1.第(2)问联立方程运算出错;
已知





27.证明:数列{
28.若对一切



正确答案
令



而对于

若


若


因此,在区间








故数列


解析
见答案
考查方向
解题思路
由题

易错点
字母太多,导致感觉混乱没有思路;
正确答案
解析
对一切


设



当



当



因为



因此


故实数a的取值范围是
考查方向
解题思路
由题问题等价于



易错点
不会构造函数