文科数学 2012年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1. 若则=（）

A{2，4}

B{2，4，6}

C{1，2，4，6}

D{1，2，3，4，5}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数图象及其与指数的关系

题型：单选题

分值: 5分

2. 曲线y=x3+11在点P(1,12)处的切线与y轴交点的纵坐标是（）

A－9

B－3

D15

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：单选题

分值: 5分

3. 如果命题“”是假命题，则在下列各结论中，正确的为（）

①命题“”是真命题；

②命题“” 是假命题；

③命题“”是真命题；

④命题“”是假命题。

A②③

B②④

C①③

D①④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

分值: 5分

4. 若函数与函数在[]上的单调性相同,则的一个值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：单选题

分值: 5分

8. 已知，，则的值为（）

D或

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

9. 为正实数，的等差中项为A；的等差中项为；的等比中项为，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：单选题

分值: 5分

10. 已知且，则必有（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的最值

题型：单选题

分值: 5分

7. 在数列中,,则该数列中相邻两项的乘积是负数的（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的定义域

题型：单选题

分值: 5分

5. 给出四个函数，分别满足：

①；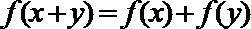

②；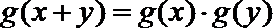

③；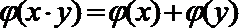

④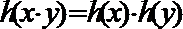。又给出四个函数的图象(如图)，则正确的匹配方案是（）

A①－甲，②－乙，③－丙，④－丁

B①－乙，②－丙，③－丁，④－甲

C①－丙，②－甲，③－乙，④－丁

D①－丁，②－甲，③－乙，④－丙

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数图象及其与指数的关系

题型：单选题

分值: 5分

12. 设，则的最小值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

扇形面积公式

题型：单选题

分值: 5分

6. 若非零向量满足，则与的夹角为（）

A30°°

B60°

C120°

D150°

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用基本不等式求最值

题型：单选题

分值: 5分

11. 平面上三点不共线，设,则的面积等于（）

D以上答案都不对

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量的模平面向量数量积的运算向量在几何中的应用

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

13. 不等式的解集为_______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像与性质

题型：填空题

分值: 5分

14. 已知函数在一个周期内的图象如图所示，则它的解析式为_______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

15. 若点到直线的距离为4，且点在不等式＜3表示的平面区域内，则=_________。

正确答案

－3

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

分值: 5分

16. 在平面直角坐标系中，双曲线C的中心在原点，它的一个焦点坐标为，、分别是两条渐近线的方向向量。任取双曲线C上的点，若（、），则、满足的一个等式是_________。

正确答案

4ab1

解析

解析已在路上飞奔，马上就到！

知识点

实际生活中的线性规划问题

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 10分

17. 求函数的最大值和最小值。

正确答案

∵，∴

∴，即的最大值为，最小值为。

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

题型：简答题

分值: 12分

18. 甲、乙两校各有3名教师报名支教，其中甲校2男1女，乙校1男2女。

（Ⅰ）若从甲校和乙校报名的教师中各任选1名，求选出的2名教师性别相同的概率；

（Ⅱ）若从报名的6名教师中任选2名，并求选出的2名教师来自同一学校的概率。

正确答案

（I）设“从甲校和乙校报名的的教师中任选一名，选出的2名教师性别相同”为事件A，则；

（II）设“从报名的6名教师中任选2名，选出的2名教师来自同一学校”为事件B，则。

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义

题型：简答题

分值: 12分

20. 如图，在四面体中，平面ABC⊥平面，

（Ⅰ）求四面体ABCD的体积；

（Ⅱ）求二面角C-AB-D的平面角的正切值。

正确答案

（I）过D作DF⊥AC于F，由平面ABC⊥平面ACD知，DF⊥平面ABC，即DF是四面体ABCD的面ABC上的高。设G为CD的中点，则由AC＝AD，知AG⊥CD，从而。

由，得。

在中，，所以。

所以四面体ABCD的体积。

（II）过F作FE⊥AB于E，连结DE，由三垂线定理，得DE⊥AB，所以∠DEF为二面角C－AB－D的平面角。

在中，，

在中，EF//BC，从而EF：BC＝AF：AC，所以，

在中，，即所求二面角的正切值为。

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 12分

21. 已知函数的图象关于原点对称，，为实数，

（1）求，的值；

（2）证明：函数在上是减函数；

（3）时，不等式恒成立，求实数的取值范围。

正确答案

(1)∵的图象关于原点对称，

∴对一切实数均成立，即

对恒成立，

比较系数，得

(2)由(1)知，，

∴，由，得，

∴函数在上是减函数；

(另证) (设，则

∵

∴，∴，

∴，即，

∴函数在上是减函数；

(3)由(2)知，函数在上是减函数，

∴在区间上，，

∴在区间上，不等式恒成立，就是

成立，又由(1)知

∴，即或，

∴，即的取值范围是。

解析

解析已在路上飞奔，马上就到！

知识点

一元高次不等式的解法

题型：简答题

分值: 12分

19. 已知正项数列的前项和满足：；设，求数列的前项和的最大值。

正确答案

当时，，所以，即，∴；

当时，由，得……①，

∴……②

两式相减，得

整理，得，

∵，∴，

∴，

∴是以1为首项，以2为公差的等差数列，

∴，

∴,又

∴是等差数列，且，公差，

∴，

∴当时，取最大值，但，

∴当时最大，最大值为。

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的最值

题型：简答题

分值: 12分

22. 如图，椭圆的中心为原点0，离心率，一条准线的方程是

（Ⅰ）求该椭圆的标准方程；

（Ⅱ）设动点P满足：，其中M、N是椭

圆上的点，直线OM与ON的斜率之积为。问：是否存

在定点F，使得与点P到直线：的距离之

比为定值；若存在，求F的坐标，若不存在，说明理由。

正确答案

（I）由，得，故椭圆的标准方程为。

（II）设，则由直线OM与ON的斜率之积为，得。

由得

，即。

∵点M、N在椭圆上，∴

∴

即，

∴P点是椭圆上的点，该椭圆的右焦点为，离心率，准线：。根据椭圆的第二定义知，存在点使得与

点P点到直线的距离之比为定值。

解析

解析已在路上飞奔，马上就到！

知识点

分式不等式的解法

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷