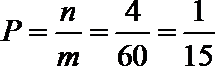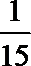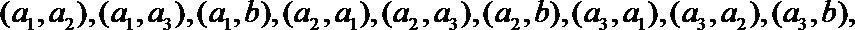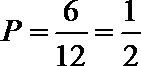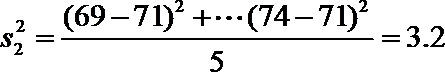- 真题试卷
- 模拟试卷
- 预测试卷
3.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.给出命题:
(1)在空间里,垂直于同一平面的两个平面平行;
(2)设





(3)已知




(4)



其中正确命题个数是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.一个算法的程序框图如图所示,若该程序输出的结果为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.一个几何体的三视图如图所示,那么此几何体的侧面积(单位:cm2)为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. △ABC的外接圆的圆心为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.给出下列命题:
①函数
②若向量a、b、c满足a·b=a·c且
③把函数
④若数列
其中正确命题的序号为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知数列{




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.化简
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有30人,则n的值为________.
正确答案
100
解析
解析已在路上飞奔,马上就到!
知识点
15.等比数列







正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,P是双曲线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知向量




正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量m


(1)若

(2)在锐角△ABC中,角A,B,C的对边分别是


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某中学的高二(1)班男同学有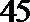
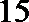
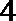
(Ⅰ)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(Ⅱ)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出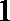
(Ⅲ)试验结束后,第一次做试验的同学得到的试验数据为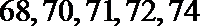
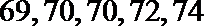
正确答案
解:(Ⅰ)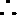
设有

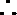
(Ⅱ)把
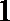
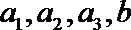
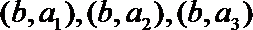

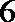
(Ⅲ)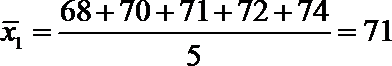
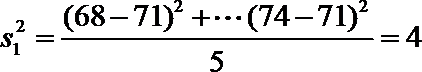
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.
(1)求证:A1D⊥平面BB1C1C;
(2)求证:AB1∥平面A1DC;
(3)求二面角D-A1C-A的余弦值.
正确答案
(1)证明:因为侧面均为正方形,
所以
所以


因为


又因为



因为


(2)
证明:连结



因为


又



所以
因为



所以

(3)解: 因为侧面


所以

设


设平面




取

又因为




因为二面角
所以,二面角

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
①当

②若函数


③当


正确答案
解:①

当


∴


∴
②
若




令


∴
若



综上,

③

当
当


令

设


且A、B两点在


∴
即实数
解析
解析已在路上飞奔,马上就到!
知识点
20.已知定点

(1)求动点E的轨迹方程;
(2)设直线


正确答案
解:(1)由题知

又



(2)设
将直线



又
依题意有

由①②可得


设O到直线

当



解析
解析已在路上飞奔,马上就到!
知识点
请考生必须在22、23题中任选一题做答。
22.
在
(1)求证:
(2)若AC=3,求
23.已知对于任意非零实数


正确答案
22.
解:(1)


又
(2)


23.
解:即


(1)当


(2)当


(3)当



综上

解析
解析已在路上飞奔,马上就到!