- 真题试卷
- 模拟试卷
- 预测试卷
4．如图是正三棱锥V—ABC的主视图，俯
A9
B6
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3． “
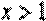
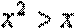
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．与向量
A
B
C
D
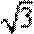
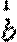
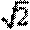
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．已知集合M={x|x<1}，N={x|2x>1}，则M∩N= （ ）
A
B{x|x<0}
C{x|x<1}
D{x|0<x<1}
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．将函数y=sin(2x+
A向右平移
B向右平移
C向左平移
D向左平移
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．等差数列{an}中，a4+a10+a16=30，则a18
A
B
C10
D20
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知a,b为两条不同直线， 
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．若函数f(x),g(x)分别是R上的奇函数、偶函数且满足f(x)+g(x)=ex，则有（ ）
Af(2)<f(3)<g(
Bg(
Cf(3)<f(2)<g(
Dg(
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.已知椭圆
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10.已知可导函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11.已知某商
正确答案
1211
解析
解析已在路上飞奔，马上就到！
知识点
14．在△ABC中，角A、B、C所对的边分别为a
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．设f(x)=
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．要建造一个面积为432m2的矩形花坛，在花坛左右两侧各留2m的人行道，前后各留1.5m的人行道，则总面积最小为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15.圆C与圆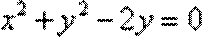 
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．设集合
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16. 已知函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，BC=CC1=AC=
（1）求证：BC1⊥平面AB1C
（2）求二面角B-AB1-C的大小
（3）求三棱锥A1-AB1C的体积
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21.已知函数
（1）求
（2）若函数
（3）在(Ⅱ)的条件下，是否存在实数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18. A、B是单位圆O上的动点，且A、B分别在第一、二象限，C是圆O与轴正半轴的交点， 
（1）若A点的坐标为
（2）求
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．等差数列{
（1）求
（2）求证：
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
22．如图，在直角坐标系
（1）求以
（2）过点E（0，
（ⅰ）当
（ⅱ）问是否存在直线，使
正确答案
解析
解析已在路上飞奔，马上就到！