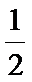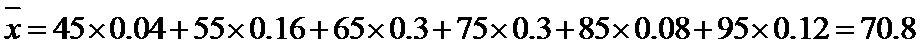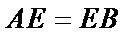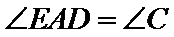- 真题试卷
- 模拟试卷
- 预测试卷
1.若

正确答案
解析
易知

考查方向
解题思路
先化简,再求值。
易错点
化简过程中容易出错。
知识点
2.
正确答案
解析
由半角公式知
考查方向
解题思路
直接利用辅助角公式即可求值。
易错点
对半角公式不熟悉导致出错。
知识点
6.执行如图所示的程序框图,则输出的
正确答案
解析
当i=1时,s=2,i=2<3,当i=2时,s=6,i=3不大于3,继续循环,此时s=15,i=4>3,终止循环,输出S值,所以本题选择B选项。
考查方向
解题思路
根据输入的值,逐一进行判断即可求解。
易错点
对循环终止条件判断失误导致出错。
知识点
7.从


正确答案
解析
依据题意画出图如下所示,则满足条件的概率为
考查方向
解题思路
依据题意画出图,根据几何度量即可求解。
易错点
不知选择哪种几何度量导致出错。
知识点
8.公比不为




正确答案
解析
由









考查方向
解题思路
先根据已知条件求出首项和公比,再求和。
易错点
相关知识点不熟悉导致出错。
知识点
3.已知集合


正确答案
解析
由



考查方向
解题思路
先求集合B,再求交集。
易错点
忽略对数函数的定义域导致出错。
知识点
4.设函数

正确答案
解析
由-2<0知知
考查方向
解题思路
根据自变量的取值范围,代入相应的解析式即可求值。
易错点
忽略分段函数的定义域导致出错。
知识点
5.若双曲线的顶点和焦点分别为椭圆
正确答案
解析
易知椭圆的焦点为(±1,0),顶点为(0,±1)和


考查方向
解题思路
根据题意求出双曲线的顶点、焦点,再利用定义求出其方程。
易错点
对双曲线及抛物线的定义混淆导致出错。
知识点
9.函数
正确答案
解析
易知该函数为偶函数,排除A,C当x趋近于正无穷大时,函数值大于零,排除D,故选择B选项。
考查方向
解题思路
根据函数的定义域、单调性、奇偶性进行判断。
易错点
相关知识点不熟悉导致出错。
知识点
10.已知函数


正确答案
解析







考查方向
解题思路
由A∩B=A知
易错点
相关知识点不熟悉导致出错。
知识点
11.如图,网格纸上小正方形的边长为
正确答案
解析
易知,该四面体的原图为

考查方向
解题思路
先由三视图还原几何体,再根据几何体的形状求其体积。
易错点
不能由三视图还原原图导致出错。
知识点
12.已知数列


正确答案
解析
由






考查方向
解题思路
由

易错点
不能求出
知识点
16.设点




正确答案
解析
试题分析:设C为圆心,依题意知






考查方向
解题思路
将
易错点
相关知识不清楚导致出错。
知识点
13.在正六边形
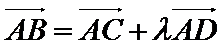

正确答案
解析
试题分析:依题意可知


考查方向
解题思路
直接运用向量的运算律进行计算。
易错点
对向量的运算率不熟悉导致出错。
知识点
14.若



正确答案
解析
试题分析:画出可行域,如下图所示,作出直线
考查方向
解题思路
画出可行域,作出直线
易错点
不能准确画出可行域导致出错。
知识点
15.已知三棱锥




正确答案
解析
试题分析:根据题意可知当三条侧棱




考查方向
解题思路
根据题意可知当三条侧棱互相垂直时侧面积之和最大,进而求出球的表面积。
易错点
不知何时三个侧面积之和最大导致出错。
知识点
17.在



(1)求
(2)若


正确答案
(1)
解析
试题分析:本题属于正余弦定理及三角形的面积公式的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
(Ⅰ)由正弦定理,可得
∴
∴
∴

(Ⅱ)由已知

由余弦定理
∴
∴

∴

考查方向
解题思路
(1)直接利用正弦定理化边为角,进而求出角C的余弦值,从而求出C;
(2)利用三角形的面积公式及均值不等式即可求出c的最小值.
易错点
相关知识点不熟容易处错。
知识点
20.已知抛物线









(1)求
(2)若圆




正确答案
(1)


解析
试题分析:本题属于直线与圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
(Ⅰ)设

又∵以


∴

∴抛物线

(Ⅱ)设直线



∴
∴
∴圆心

∵圆


∴
∴

此时直线






圆

考查方向
解题思路
(1)利用相关知识求抛物线方程;
(2)联立方程组,综合利用题中条件即可求解.
易错点
对题中条件的处理容易出错。
知识点
18. 如图,在四棱锥





(1)求证:
(2)若平面




正确答案
(1)见证明;(2)
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
证明:取


∴
∵
∴
∵




∴平面
∵
∴
(Ⅱ)∵平面

∴
∵
∴平面
∴在







设点


则有
∴


考查方向
解题思路
(1)直接利用线面平行的判定定理进行证明;
(2)利用作出高,再利用体积公式即可求解.
易错点
相关定理不熟容易处错。
知识点
19.在一次数学考试中,数学课代表将他们班
(1)在答题卡上作出这些数据的频率分布直方图;
(2)估计该班学生数学成绩的中位数和平均值;
(3)若按照学生成绩在区间
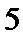
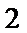
正确答案
(1)见解析;(2)

解析
试题分析:本题属于用样本估计总体与古典概型综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
(Ⅰ)
(Ⅱ)由频率分布直方图可得该班学生数学成绩的中位数为70;
该班学生数学成绩的平均值为
(Ⅲ)由题可得在抽取的5个样本中属于不及格、及格、优良三个等次的个数分别为1、3、1,对应编号分别为

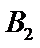


从中任意抽取2名学生的情况有

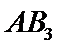
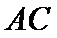





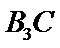
其中至少有一名学生成绩属于及格等次的情况有9种
∴至少有一名学生成绩属于及格等次的概率为
考查方向
解题思路
(1)由表中数据直接绘制直方图;
(2)利用频率分布直方图求中位数和平均值;
(3)用样本的频率代替概率,利用古典概型求概率.
易错点
相关知识点不熟容易处错。
知识点
22.选修4-1:几何证明选讲
如图,点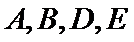



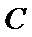



(1)证明:弧

(2)若
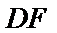
正确答案
(1)见解析;(2)
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
(Ⅰ)证明:∵
∴
∵
∴
∵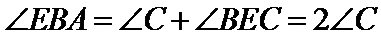
∴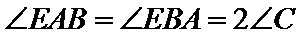
∴
∴
∴
(Ⅱ)由(Ⅰ)知
∴
∴
又∵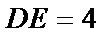
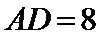
∴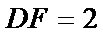
考查方向
解题思路
(1)利用圆的割线的性质及角的关系即可得证;
(2)利用三角形司相似即可求DF的长.
易错点
相关定理不熟悉导致本题失分。
知识点
21.设函数



(1)求
(2)证明:
正确答案
(1)
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
(Ⅰ)∵
∴
又点

∴
∴

(Ⅱ)由(Ⅰ)知
又∵

且
∴存在

当


∴
由
∴
综上,对任意

考查方向
解题思路
(1)直接利用导数的几何意义即可求出函数的解析式;
(2)先判断函数的单调性,再利用导数证明.
易错点
第二问对题中所给条件不知如何下手导致失分。