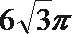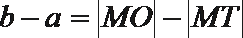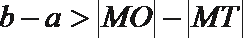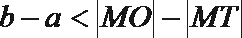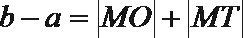- 真题试卷
- 模拟试卷
- 预测试卷
1.设全集



正确答案
解析



考查方向
本题主要考查了集合的概念和运算,在近几年的各省高考题中是必考题 ,常与不等式、函数、方程等知识点交汇命题。
解题思路
法一:分步求

法二:用公式
易错点
1、概念不清导致错误。2、运算出错。
知识点
3.若实数数列:

正确答案
解析
由


考查方向
本题主要考查等比数列的概念和椭圆的离心率的概念。
解题思路
由等比数列求出a,代入圆锥曲线方程求出离心率。
易错点
1、等比数列概念不清导致a 漏负解
2、误认为圆锥曲线只是椭圆导致漏解。
知识点
4.函数





正确答案
解析
定点A(1,-1)在直线
考查方向
本题主要考查函数过定点问题及最值问题
解题思路
求出定点A,得出m,n的关系m+n=1,再用乘1法
易错点
1、定点A求不出来;
2、最值求解的基本方法不熟悉。
知识点
7.已知条件
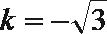
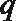
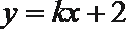
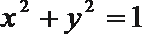
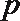
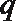
正确答案
解析
直线和圆相切由d=r得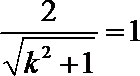
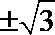
考查方向
本题主要考查充要条件的概念及直线 和圆的位置关系。
解题思路
直线和圆相切得出k值,再进行判断。
易错点
充要条件的概念不清。
知识点
8.平面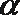


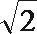
正确答案
解析
由题设截面圆圆心为H,则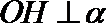
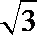
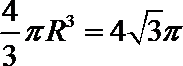
考查方向
本题主要考查球的相关知识。
解题思路
画出图形,归结到直角三角形中解决问题
易错点
不能画出正确图形,归结到直角三角形中解决问题。
知识点
10.若函数

正确答案
解析



考查方向
本题考查函数与导数相关的知识。
解题思路
求导,求出极值点,由图可以看出一个极大值点大于1,一个极小值点小于-1。得出m的范围。
易错点
1、不理解极值与导数的关系。
2、求导运算出现问题。
知识点
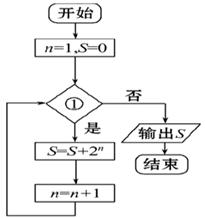
9.若如图所示的程序框图输出的

正确答案
解析
126=2+

考查方向
本题考查流程图的知识。
解题思路
根据循环体写出输出的结果的形式,求出n的值 。
易错点
不理解流程图的逻辑含义;
知识点
2.已知复数


正确答案
解析
考查方向
本题主要考查复数的运算。
解题思路
直接代入计算
易错点
运算出错。
知识点
5.如图为某几何体的三视图,则该几何体的表面积为( )
正确答案
解析
这个是底面是边长为2的正方形和半径为1的圆的组合图形,高为2的柱体,所以侧面积为
考查方向
本题主要考查大概三视图及几何体的表面积知识
解题思路
正确画出几何体,求出表面积。
易错点
1、空间想象能力弱,画不出几何体的形状。
2、柱体的表面积公式不熟悉导致结果出错。
知识点
6.气象意义上从春季进入夏季的标志为:“连续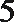
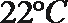
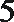
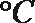
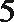
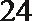
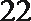
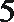
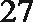
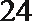
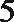
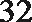
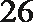
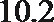
正确答案
解析
①中至少有两个整数22,故后面两个数大于24,②中易举反例19,20,27,27,27。③中设另外四个数分别为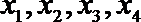
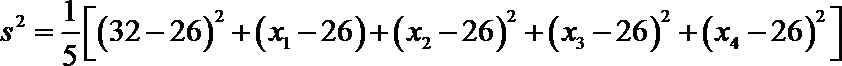
考查方向
本题主要考查大概三视图及几何体的表面积知识
解题思路
对每组数据分别分析。
易错点
1、特征数的概念不清。
2、分析处理数据的能力不强。
知识点
11.过双曲线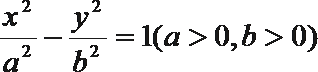
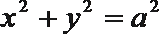
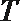
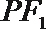
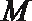
正确答案
解析
连结P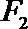
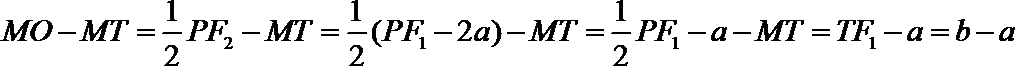
考查方向
本题考查学生的解析几何的综合运用的能力。
解题思路
将已知线段向焦半径转化,利用双曲线的性质解决。
易错点
1、不能正确地将已知条件进行转化;
2、解决综合问题的能力不强。
知识点
12.已知函数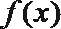
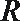
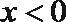
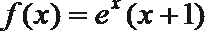
①当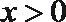
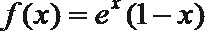
②函数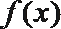
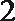
③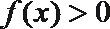
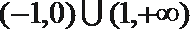
④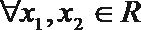
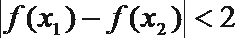
其中正确的命题是( )
正确答案
解析
当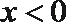
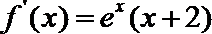
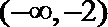
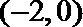
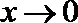
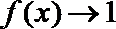
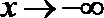
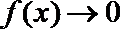
考查方向
本题主要考查函数的综合应用
解题思路
正确画出函数的图象。
易错点
1、函数性质理解不透;
2、不能正确的分析出函数的基本形式。
知识点
17. 在







(Ⅰ)求证:
(Ⅱ)若


正确答案
(Ⅰ)略;(Ⅱ)
解析
解:(Ⅰ)由条件:
由于:
所以:
(Ⅱ)


又:
由

所以:
考查方向
本题考查了三角函恒等变换及解三角形的有关知识,注意降幂公式的运用。第二问中要注意将角的关系和面积关系向边的关系的转化。
解题思路
第一小题中先降幂,再由余弦定理将角转化为边的关系;第二小题中由余弦求出正弦,再由面积得出边的关系;再由余弦定理得出另一个边的关系。从而求出b 的值。
易错点
第二问中由余弦值求正弦值不要忽略角的范围的限制,
知识点
16.若




















正确答案
②④
解析
①中

考查方向
本题主要考查学生接受新概念的能力及综合运用数学知识解决数学问题的能力。
解题思路
分别对每个选项进行考虑,验证排除,得出结果。
易错点
1.不能正解理解给定定义的意义。
知识点
18. 如图所示,该几何体是由一个直三棱柱



(Ⅰ)证明:平面

(Ⅱ)求正四棱锥


正确答案
略
解析
(Ⅰ)证明:直三棱柱









(Ⅱ)




考查方向
本题考查了立体几何中的面面垂直的证明和正四棱锥的体积问题,
解题思路
本题第一问证明面面垂直,只要证明线面垂直即可;第二问把两个几何体的体积求出来,由两个几何体的体积关系直接求出高就行了。
易错点
1、解题 的规范化问题,2、第二问中不能正确的求出所需几何体的体积。
知识点
20. 椭圆









(Ⅰ)求椭圆

(Ⅱ)设














正确答案
(Ⅰ)



解析
题 是解析几何中的常规题,两个椭圆的组合给学生解题带来很大的心理压力,只要能突破这一障碍,总体来讲难度还是不大的。
(Ⅰ)依题意




由对称性,四个焦点构成的四边形为菱形,且面积
解得:
所以椭圆


(Ⅱ)(1)设



所以:



(2)设



所以:
同理:



结合(1)有
考查方向
考查了椭圆方程的求法,以及椭圆中的定值问题,对学生的运算和思维能力要求较高。两个椭圆组合起来,显得条件较多,对学生的解题形成很大的干扰。
解题思路
本题考查椭圆的性质及运用,解题步骤如下:1、设出椭圆的方程,由两个条件得出两个方程,解方程组。2、设动点求斜率之积为常数;
易错点
1、不能正确的设出两个椭圆的方程,
2、(2)(3)问中运算量较大,可能出错。
知识点
13.向量




正确答案
解析
由



考查方向
本题主要考查向量的相关知识。
解题思路
将垂直条件转化为数量积为0,代入数据求出
易错点
1.不能将垂直的条件进行转化。
2.夹角公式不清楚
知识点
14.已知


正确答案
解析
由



考查方向
本题主要三角函数及三角恒等变换的相关知识。
解题思路
将垂直条件转化为数量积为0,代入数据求出
易错点
1.忽略角的范围导致错误;2.公式不能灵活运用。
知识点
15.若


正确答案
-1
解析
画出可行域,得出当x=1,y=1时z的最小值为-1
考查方向
本题主要考查线性规划的相关知识。
解题思路
画出可行域,找出最优解
易错点
不能正确画出可行域。
知识点
19. 甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的
(Ⅰ)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(Ⅱ)现要从中选派一人参加该项竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
正确答案
(1)
解析
本题属于概率统计中中的基本题型,难度不大。(1)直接按照步骤来求(2)要列出基本事件
。(Ⅰ)记甲被抽到的成绩为

用数对






















基本事件总数
事件A包含的基本事件:









事件

所以
(Ⅱ)派甲参赛比较合适.理由如下:





考查方向
本题考查了茎叶图、古典概型及特征数的相关知识。
解题思路
1.从茎叶图中看出两人的成绩,列出总的基本事件数共有25 个,找出甲比乙成绩高的事件数,从而得出概率。
2.分别求出两人的平均成绩和方差进行比较。
易错点
1、求总的等可能基本事件数出错;
2、选派的标准是什么学生把握不准。
知识点
21. 设函数

(Ⅰ)当

(Ⅱ)当

正确答案
函数单调减区间为:(Ⅰ)

解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)涉及恒成立问题,转化成求函数的最值,这种思路是一般解法,往往要利用“分离参数法”;(3)零点回代是对学生是一种较高的要求.
(Ⅰ)函数

当


得:

所以函数单调增区间为:
,得:
所以函数单调减区间为:
(Ⅱ)若证

即:

设

显然





使得:













∵


∴
考查方向
本题考查了利用导数求函数单调区间的知识,第二问是证明题,过程中要对不等式进行等价变形,本题难在求导后零点不好求,要由零点定理对导数的零点进行分析,将零点关系式回代原函数,求出原函数的正负。
解题思路
1、求导,然后解导数不等式,算极值。
2、对不等式进行等价变形,转化为一个常见函数再进行求导;
3、零点回代。
易错点
1、第二问中卡在求导后解不出零点。2、设出零点后得出零点关系式代入原函数后的正负难以判断。
知识点
22. 如图,














(Ⅰ)

23. 在直角坐标系中,曲线








(Ⅰ)求点






24. 已知函数
(Ⅰ)若



正确答案
22.略
23. (Ⅰ)
24. (Ⅰ)

解析
22. (Ⅰ)证明:连接


因为:

由弦切角等于同弦所对的圆周角:
所以:



(Ⅱ)由切割线定理得:
因为
所以:
由相交弦定理得:
所以:
23. (Ⅰ)由极值互化公式知:点




消去参数


(Ⅱ)点

将直线的参数方程代入曲线

设其两个根为

所以:

由参数

24. (Ⅰ)当
解得:
所以原不等式解集为
(Ⅱ)

只需:
解得:

考查方向
22.几何证明的相关知识
23. 参数方程和极坐标第
24. 本题考查了绝对值不等式的运用
解题思路
22.运用同圆中同弧或等弧所对的角相等,第二题中运用相交弦定理和切割线定理解决,注意进行线段关系的转化。
23. 按步骤解题
24.无
易错点
22.1.解题不规范 2.出边和角的关系。
23. 基础知识不扎实倒致错误。
24. 绝对值不等式不会运用