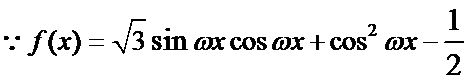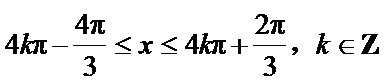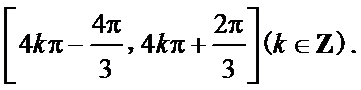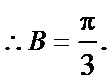- 真题试卷
- 模拟试卷
- 预测试卷
1.在复平面内,复数(1+
正确答案
解析


考查方向
解题思路
判断复数对应的点所在的位置,只要看出实部和虚部与零的关系即可,把所给的式子展开变为复数的代数形式,得到实部和虚部的取值范围,得到结果.
易错点
1、本题易在计算上发生错误,弄错
2、本题不容易理解复数的实部与虚部与坐标象限的关系。
知识点
2.已知集合A={x|y=

正确答案
解析
由






考查方向
解题思路
利用定义域所满足的条件得出集合A中X所满足的关系,解不等式得到集合B中y所满足的关系,然后求两个集合的交集.
易错点
1、本题易在解不等式上出错,搞不清集合的交并补运算 。
2、本题易搞不清楚是求定义域还是值域。
知识点
5.执行如图所示的程序框图.若输出的结果为3,则可输入的实数x的个数为( )
正确答案
解析
根据题意,该框图的含义是
当x≤1时,得到函数y=x2-1;当x>1时,得到函数y=log2x.
因此,若输出结果为3时,
①若x≤1,得x2-1=3,解之得x=-2
②当x>1时,得y=log2x=3,得x=8
因此,可输入的实数x值可能是-2或8,共2个数
故选:B
考查方向
解题思路
根据题中程序框图的含义,得到分段函数
易错点
1、本题易在由x2-1=3,解之得x=±2 。但是易忘掉x≤1的条件,舍掉2.
2、本题不容易搞清楚程序框图的含义。
知识点
7.设α为平面,a、b为两条不同的直线,则下列叙述正确的是( )
正确答案
解析
对于A答案,直线a与b可以相交,也可以异面,也可以平行;
对于B答案,b和a垂直,但是和平面α的关系不能确定,也可以在平面α内;
对于D答案,b和a垂直,但是和平面α的关系不能确定,可以和平面α斜交。
所以,A选项不正确, C选项不正确,D选项不正确,B选项正确。
考查方向
解题思路
1.对每一个选项进行判断即可;
2.也可以画出图形,直接判断。
A选项不正确, C选项不正确,D选项不正确,B选项正确。
易错点
本题在线线平行、线面平行,线线垂直、线面垂直上容易混淆。有些关系没有考虑到导致出错。
知识点
9.已知抛物线C:y2 =8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若FP=3FQ,则|QF|=( )
正确答案
解析
设Q到l的距离为d,则|QF|=d
由FP=3FQ,可以得到直线PF的斜率为
所以,直线PF的方程为
再根据图形可以得出QF的长是
考查方向
解题思路
1.画出图形,找出直线PF的斜率,求出直线方程;
2.把直线PF的方程和抛物线的方程联立,求出点Q的横坐标;
3.由点Q的横坐标和点F的横坐标求出QF的长。B选项不正确, C选项不正确,D选项不正确,A选项正确。
易错点
本题容易在找直线PF与x轴的夹角时出错,即在求直线PF的斜率时容易出错;再者就是计算出错。
知识点
3.已知命题p:函数f (x)=|cosx|的最小正周期为2π;命题q:函数y=x3+sinx的图像关于原点中心对称,则下列命题是真命题的是( )
正确答案
解析
f (x)=cosx的最小正周期为π,f (x)=|cosx|的最小正周期为π,命题p为假。
函数y=x3是奇函数,函数y=sinx是奇函数,所以函数y=x3+sinx是奇函数,图像关于原点中心对称。命题q真。所以A.p






考查方向
本题主要考查了三角函数的图象与性质,三角函数的周期性及其求法;复合命题的真假;正弦函数的对称性,在近几年的各省高考题出现的频率较高,常与三角恒等变形公式,函数单调性、周期性、对称型、奇偶性等知识点交汇命题。
解题思路
f (x)=cosx的最小正周期为π,f (x)=|cosx|的最小正周期为π。函数y=x3+sinx是奇函数,图像关于原点中心对称。
易错点
1、本题易在求最小正周期上出现错误,不会判断函数的奇偶性。
2、本题易在判断复合命题的真假上出错。
知识点
4.已知变量x与y正相关,且由观测数据算得样本平均数x=3,y=3.5,则由该观测数据算得的线性回归方程可能是( )
正确答案
解析
∵变量x与y正相关,∴可以排除A,D;因为回归直线方程恒过样本中心点样本将平均数x=3,y=3.5,代入,C符合,B不符合,故选:C
考查方向
解题思路
变量x与y正相关,所以x前边的系数为正,再利用回归直线方程恒过样本中心点是关键。
易错点
1、本题易在判断x,y的正负相关关系上出错 。
2、本题不容易搞清楚样本平均数与线性回归方程的关系。
知识点
6.已知函数f(x)= 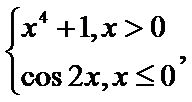
正确答案
解析
当x=1,f(1)=2,当x=-1,f(-1)=cos(-2)=cos2.所以A错。事实上,在不对称的区间上都是没有奇偶性的;
函数y=cos2x在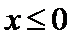
函数y=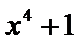
函数y=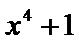
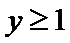
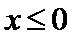
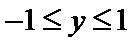
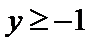
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
1.对每一个选项进行判断即可;
2.也可以画出图像,直接判断。
A选项不正确, B选项不正确, C选项不正确,D选项正确。
易错点
1、本题不容易想到在x>0时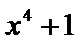
2、对于cos2x在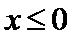
3、整个函数在定义域中的值域是求它们的交集容易出错。
知识点
8.若等比数列的各项均为正数,前4项的和为9,积为
正确答案
解析
因为等比数列的各项均为正数,前4项的和为9,积为
所以,设此等比数列的首项为a1 ,公比为q
前4项之和为S,前4项之积为P,前4项的倒数和为M
若q=1,则
若
所以,
又因为前4项的和为9,积为
所以答案选D
考查方向
解题思路
1.对条件进行展开、变形;
2.设出前4项倒数的和M,对前4项的和与积这三个量进行转化,变形,整理从而得出结果。
A选项不正确, B选项不正确,C选项不正确,D选项正确。
易错点
本题给出两个条件,容易想到求出等比数列的基本量a1和q,但是在求解的时候就发现很不容易。
知识点
10.如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为( )
正确答案
解析
由三视图画出直观图,这是一个倒下放置的四棱锥,底面是正视图,
面积是
高是侧视图的下底长2
所以,四棱锥的体积是
考查方向
解题思路
1.画出直观图;
2.这是一个倒下放的四棱锥,由四棱锥的体积公式直接计算;
A选项不正确, B选项不正确,D选项不正确,C选项正确。
易错点
1.在由三视图画直观图的时候观察不出来;
2.由体积公式进行计算时出错。
知识点
11.已知点P在直线x+3y-2=0上,点Q在直线x+3y+6=0上,线段PQ的中点为M(x0,y0),且y0
正确答案
解析
因为PQ的中点为M,可以得出点M的轨迹就是x+3y+2=0与直线x+3y+6=0间的平行直线x+3y+2=0;又因为y0
由
则
所以


A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
1、首先由直线x+3y+2=0与直线x+3y+6=0是平行线,得出PQ的中点M(x0,y0)满足的直线方程;
2、根据y0<x0 +2求出对应的射线范围,即进一步限定点M的范围;
3、结合
A选项不正确, B选项不正确, C选项不正确,D选项正确。
易错点
1、本题不容易想到点M的轨迹就是与直线x+3y-2=0和x+3y+6=0等距离的直线 。
2、本题在求解出直线与x+3y+2=0与直线x-y+2=0的交点后,求解斜率的范围时候容易出错。
3、端点处的讨论容易考虑不全。
知识点
12.已知函数f(x)= 
正确答案
考查方向
解题思路
1、首先画出函数y=|f(x)|和y=ax的图像;
2、讨论a的范围;
易错点
1、本题两个函数的图像画不出来,图像画出后不容易进行对称变换;
2、在分析参数a的取值问题上容易出错;
3、在a<0时,用导数求解具体值的时候出错。
知识点
14.已知向量a=(1,

正确答案
2
解析
根据a=(1,

所以
即
考查方向
解题思路
本题考查平面向量的有关问题,
解题步骤如下:根据向量的坐标表示写出

易错点
1、向量模的求解出错;
2、向量的数量积的定义理解出错。
知识点
13.已知函数f(x)= 
正确答案
4
解析
1、将-4代入
2、将16代入
考查方向
本题主要考查了
1、分段函数的求值问题;
2、指数函数的求值;
3、复合函数的求值。
解题思路
本题考查复合函数、分段函数的求值问题,属于较为简单的类型。
解题步骤如下:1、将-4代入第二个式子,先求f(-4)的值16;
2、再将16代入第一个式子求出最终的值.
易错点
1、对复合函数内层、外层函数的理解出错;
2、代入求值时计算出错。
知识点
15.已知双曲线
正确答案
解析
已知

所以

考查方向
解题思路
本题考查双曲线的几何性质,
解题步骤如下:根据双曲线的离心率写出e与a、b的关系;分离出a、b的关系,进而得到渐近线的斜率;
写出渐近线方程。
易错点
1、双曲线的离心率e与渐近线的斜率之间的转化出错;
2、双曲线的渐近线的理解出错。
知识点
16.数列{an}的前n项和为Sn,若Sn-Sn一1=2n-l (
正确答案
5
解析
由条件Sn-Sn一1=2n-l (
当n=3时,S3-S2=2×3-1=5,即a3=5
所以a1+a3=5
考查方向
解题思路
本题考查数列递推式,解题步骤如下:
根据条件求出S1= a1=0;2. 再根据S3-S2=a3求出a3.即可得到答案
易错点
对递推式不熟悉,代入的时候出错。
知识点
18.如图,四棱锥S- ABCD中,SD⊥底面ABCD,AB//DC,AD ⊥ DC,,AB=AD=1,DC=SD=2,M.N分别为SA,SC的中点,E为棱SB上的一点,且SE=2EB.
(I)证明:MN//平面ABCD;
(II)证明:DE⊥平面SBC.
正确答案
略,详见解析;
解析
试题分析:本题属于立体几何中的基本问题,具体解析如下:
证明:(Ⅰ)连


∴
又∵

∴
(Ⅱ) 连

∴
又


∴
∵

∵

又
当

在



∴
又
∴
∵
∴

考查方向
本题考查了立体几何的相关知识,大体可以分成以下几类:
1、考察线面平行的判定,由线线平行得到MN//平面ABCD;
2、线线垂直的判定;
3、三角形相似的判定;
4、线面垂直的判定等.
解题思路
本题考查立体几何中的线面平行、线面垂直,解题步骤如下:
1、由
2、在三角形中利用勾股定理判定线线垂直;
3、三角形相似得出线段成比例,再次得到三角形相似;
4、得到角相等之后再次判定三角形相似,进而得到线线垂直,最后根据线面垂直的判定得到答案。
易错点
1、线面平行的判定条件没有写全;
2、找不到线线垂直的两条直线;
3、线线垂直得到线面垂直时条件遗漏。
知识点
19.现有甲、乙、丙、丁4个学生课余参加学校社团文学社与街舞社的活动,每人参加且只能参加一个社团的活动,且参加每个社团是等可能的.
(I)求文学社和街舞社都至少有1人参加的概率;
(II)求甲、乙同在一个社团,且丙、丁不同在一个社团的概率,
正确答案
(1)概率为
(2)概率为
解析
试题分析:本题属于古典概型中的基本问题,具体解析如下:
甲、乙、丙、丁4个学生课余参加学校社团文学社与街舞社的情况如下
共有16种情形,即有16个基本事件
(I)文学社和街舞社没有人参加的基本事件有2个,概率为
(II)甲、乙同在一个社团,且丙、丁不同在一个社团的基本事件有4个,
概率为
考查方向
本题考查了古典概型的概率求解,大体可以分成以下几类:
1、基本事件的判定;
2、古典概型的判定;
3、古典概型的概率公式的应用。
解题思路
本题考查古典概型的判定和计算,解题步骤如下:
1、写出所有的基本事件;
2、找出满足条件的基本事件;
3、根据古典概型的计算公式代入运算。
易错点
1、基本事件没有写全;
2、查找满足条件的基本事件个数的时候出错;
3、利用概率公式进行运算的时候出错。
知识点
20.已知椭圆C:

(I)求椭圆C的方程;
(Ⅱ)设点B,C,D是椭圆上不同于椭圆顶点的三点,点B与点D关于原点O对称.设直线CD,CB,OB,OC的斜率分别为k1,k2,k3,k4,且k1k2=k3k4.
(i)求k1k2的值:
(ii)求OB2+ OC2的值.
正确答案
(I)所求椭圆方程为
(Ⅱ) (i)k1k2
(ii)OB2+ OC2=7
解析
试题分析:本题属于直线与圆锥曲线的综合问题,属于较难类型,主要在于计算,具体解析如下:
(Ⅰ)设椭圆

由题意,以椭圆

∴圆心到直线

∵椭圆
∴



故所求椭圆方程为
(Ⅱ)(i)设

于是
(ii)方法一由(i)知,

所以,
即

又

所以,OB2+OC2 
方法二由(i)知,


得

所以,
下同方法一
考查方向
本题考查了圆锥曲线中的有关问题,大体可以分成以下几类:
1、椭圆标准方程的求法;
2、点到直线距离公式的应用;
3、直线、圆及圆锥曲线的交汇问题;
4、运算能力的考察。
解题思路
本题考查圆锥曲线的综合问题,难度稍微有些大,问题最大的在于计算,解题步骤如下:
1、根据条件,利用点到直线的距离公式得出基本量a,b,c的关系,进而写出椭圆方程;
2、直接利用斜率的表达式计算出k1k2
3、此时方法不唯一,可以利用方程间的未知数的关系直接求出各个量的值,进而求出OB2+ OC2=7;也可以把直线方程代入椭圆方程表示出

易错点
1、题目分析得到基本量a,b,c的关系时出错;
2、k1k2的表达式写错;
3、直线方程代入椭圆方程后,计算OB2+ OC2出错。
知识点
21.已知函数f(x)=lnx-ax2一a+2.(a∈R,a为常数)
(I)讨论函数f(x)的单凋性;
(II)若存在x0∈(0,1],使得对任意的a∈(-2,0],不等式mea+f(x0)>0(其中e为自然对数的底数)都成立,求实数m的取值范围.
正确答案
(1)函数


(2)实数


解析
试题分析:本题属于函数的应用中相对较难的问题,解题思路一般,但是运算还是有一定的难度,具体解析如下:
解:(Ⅰ)函数


当



当



所以函数


(II)由(1)知道当


所以


对任意的



等价于对任意的

即对任意的

不等式

记

所以

所以实数


考查方向
解题思路
本题考查函数的性质,运用导数进行求解,解题步骤如下:
1、根据题意,对函数
2、在参数a的范围内进行不等式的求解;
3、第二问,在参数a的范围内讨论
4、分离参数,构造新的函数,求出值域,进而得到参数的取值范围。
易错点
1、导数的运算出错;
2、求解函数的值域时出错;
3、对参数a进行讨论时考虑不全。
知识点
17.已知函数f(x)=(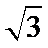
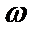
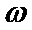
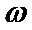
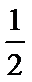
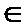
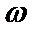
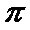
(I)求函数f(x)的单调递增区间;
(II)在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
正确答案
(1)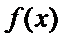
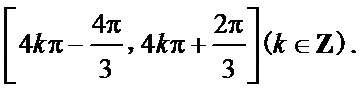
(2)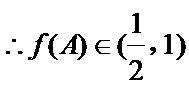
解析
试题分析:本题属于三角函数、解三角形中的基本问题,题目的难度是逐渐由易到难,具体解析如下:
(I)
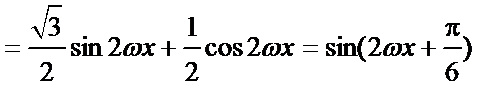
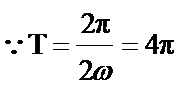
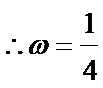
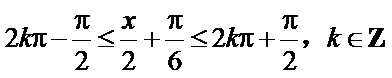
得
∴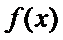
(Ⅱ)由正弦定理得,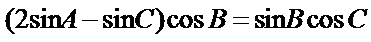

或: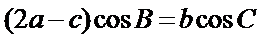
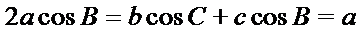
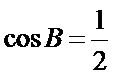
∵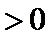
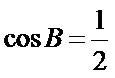
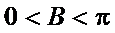
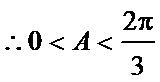

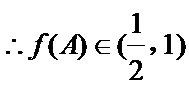
考查方向
本题考查了三角函数的化简与求值,大体可以分成以下几类:
1、由y=Asin(ωx+φ)的部分性质确定其解析式;
2、三角函数的恒等变换及化简求值;
3、正余弦定理的综合运用;
4、三角形中的几何计算;
5、三角函数的最值等.
解题思路
本题考查三角函数以及解三角形,解题步骤如下:
1、化简f(x)=(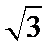
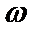

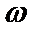
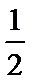
2、求函数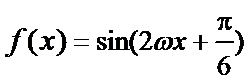
3、根据三角形内角和,利用三角恒等变换求出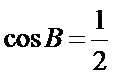
4、利用三角形内角和得出角A的范围,求出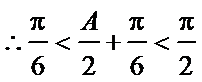
易错点
1、化简f(x)=(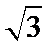
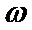


2、求单调区间时候范围不清导致出错;
3、在化简求值时,角的范围不清导致出错。
知识点
22.选修4-1:几何证明选讲
如图, 圆M与圆N交于A, B两点, 以A为切点作两圆的切线分别交圆M和圆N于C、D两点,延长DB交圆M于点E, 延长CB交圆N于点F.已知BC=5, DB=10.
(I)求AB的长;
(II)求
正确答案
(1)
(2)
解析
试题分析:本题属于平面几何问题,具体解析如下:
(Ⅰ)根据弦切角定理,
知

∴△


故
(Ⅱ)根据切割线定理,知

两式相除,得
由△



又
由(*)得
考查方向
本题考查了平面几何中圆幂定理的应用,大体可以分成以下几类:
1、圆与圆的位置关系;
2、弦切角定理的应用;
3、相似三角形的判定;
4、切割线定理的应用;
5、相似三角形的性质。
解题思路
本题考查平面几何内圆的相关知识,解题步骤如下:
1、根据弦切角定理判定三角形相似,进而得到AB的值;
2、根据切割线定理得到两边对应成比例,进而得出三角形相似;
3、根据三角形相似的性质,得到比例。
易错点
1、相似三角形的判定应用时条件不全;
2、切割线定理应用时两式相除这个技巧不容易想到;
3、运算出错。