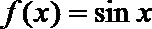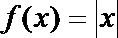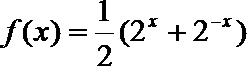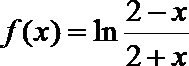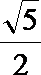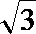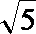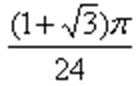- 真题试卷
- 模拟试卷
- 预测试卷
2.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 在等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
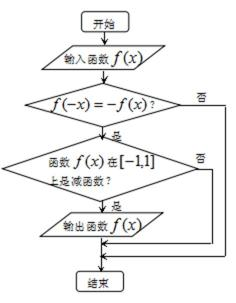
8. 如图所示的流程图,现输入以下函数,则可以输出的函数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 将正方形






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 定义运算:


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知双曲线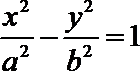
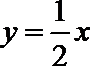
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 把边长为





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知命题



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题(14、15题,只能从中选作一题)
14.(几何证明选讲选做题)
如图,在











15. (坐标系与参数方程选做题))
已知圆







正确答案
14.
15.
解析
解析已在路上飞奔,马上就到!
知识点
11.已知

正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
13. 给出可行域 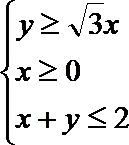
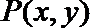
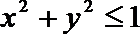
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表:
(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级;
(2)用简单随机抽样方法从这



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列


(1)判断数列
(2)求数列
(3)若数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求函数
(2)在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在三棱锥









(1)证明:

(2)求三棱锥
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆




(1)求椭圆
(2)对于





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1)求

(2)若函数


正确答案
解析
解析已在路上飞奔,马上就到!