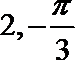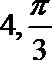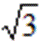文科数学德阳市2011年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

3．设向量和的长度分别为4和3，夹角为60°，则的值为（）

A37

B13

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量的模平面向量数量积的运算数量积表示两个向量的夹角

题型：单选题

分值: 5分

6．已知,函数是它的反函数,则函数的大致图象是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化指数函数的图像变换指数函数与对数函数的关系反函数

题型：单选题

分值: 5分

8．下图给出的是计算的值的一个程序框图，判断其中框内应填入的条件是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

程序框图

题型：单选题

分值: 5分

1．已知全集U={0，1，2，3，4}，集合A={1，2，3}，B={2， 4}，则(∁UA)∪B为（）

A{0，2，4}

B{2，3，4}

C{1，2，4}

D{0，2，3，4}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

交、并、补集的混合运算

题型：单选题

分值: 5分

2．设为虚数单位,则复数（）

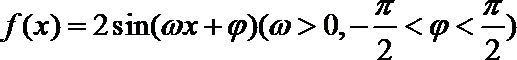
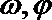
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复数代数形式的乘除运算

题型：单选题

分值: 5分

4．等比数列的前项和为．已知则=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的基本运算等比数列的性质及应用

题型：单选题

分值: 5分

5．设集合则“”是“”的（）

A充分而不必要条件

B必要而不充分条件

C充分必要条件

D既不必要也不充分条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

并集及其运算充要条件的判定

题型：单选题

分值: 5分

7．函数的部分图象如图所示,则的值分别是（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由y=Asin（ωx+φ）的部分图象确定其解析式

题型：单选题

分值: 5分

9．有下列四个命题：

①对于,函数满足,则函数的最小正周期为2；

②所有指数函数的图象都经过点；

③若实数满足,则的最小值为9；

④已知两个非零向量,,则“”是“”的充要条件．

其中真命题的个数（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用函数的周期性指数函数的单调性与特殊点数量积判断两个平面向量的垂直关系利用基本不等式求最值

题型：单选题

分值: 5分

10．设函数的定义域为A，若存在非零实数，使得对于任意,有则称为上的低调函数．如果定义域为的函数且为上的10低调函数，那么实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

绝对值不等式的解法

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

12．若，则 __________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法运用诱导公式化简求值分组转化法求和

题型：填空题

分值: 5分

13．函数在点处的切线方程为__________．

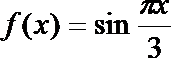
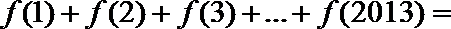
正确答案

y=4x-4

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义直线的一般式方程

题型：填空题

分值: 5分

14．已知P是△ABC所在平面内一点，，现将一粒黄豆随机撒在△ABC内，则黄豆落在△PBC内的概率是__________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量的线性运算性质及几何意义向量在几何中的应用与面积、体积有关的几何概型

题型：填空题

分值: 5分

11．在中的对边分别为，已知__________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理

题型：填空题

分值: 5分

15．设函数是定义在上的偶函数，且对任意的恒有，已知当时，则

①是函数的周期；

②在上是增函数，在上是减函数；

③的最大值是，最小值是；

④当时，

其中所有正确命题的序号是__________．

正确答案

①④

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用函数单调性的判断与证明函数的最值函数奇偶性的性质函数的周期性

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

18．某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．

（1）根据茎叶图计算样本均值；

（2）日加工零件个数大于样本均值的工人为优秀工人．根据茎叶图推断该车间12名工人中有几名优秀工人？

（3）从抽取的6名工人中，任取2人，求恰有1名优秀工人的概率．

正确答案

解：

（1）样本均值为

（2）抽取的6名工人中2名为优秀工人，所以12名工人中有4名优秀工人.

（3）抽取的6名工人中2名为优秀工人，设为A,B；4名为非优秀工人，设为a,b,c,d

从A,B,a,b,c,d中任取2人的不同取法有

（A,B）,(A,a),(A,b),(A,c),(A,d)

(B,a),(B,b),(B,c),(B,d)

(a,b),(a,c),(a,d)

(b,c),(b,d)

(c,d)共15中，其中恰有1名优秀工人的取法有

(A,a),(A,b),(A,c),(A,d)，(B,a),(B,b),(B,c),(B,d)共8种

所以，恰有一名优秀工人的概率是

解析

解析已在路上飞奔，马上就到！

知识点

古典概型的概率茎叶图众数、中位数、平均数

题型：简答题

分值: 13分

20．已知向量

（1）若，求的值；

（2）记函数在中，角的对边分别是且满足,求的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的化简求值三角函数中的恒等变换应用正弦定理平面向量数量积的运算

题型：简答题

分值: 12分

16．已知函数．

（1）求函数的最小正周期和最大值；

（2）在给出的平面直角坐标系中，画出函数在区间上的图像．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的图象三角函数中的恒等变换应用三角函数的最值

题型：简答题

分值: 12分

17．已知等差数列的前项和为，且。

（1）求数列的通项公式；

（2）求使不等式成立的的最小值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用等差数列的前n项和及其最值数列与不等式的综合

题型：简答题

分值: 12分

19．已知函数

（I）求函数的最小值；

（II）已知,命题p:关于的不等式对任意的恒成立；q:函数是增函数。若“p或q”为真，”p且q”为假，求实数的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断分段函数的解析式求法及其图象的作法函数的最值函数恒成立、存在、无解问题

题型：简答题

分值: 14分

21．设函数（是实数，为自然对数的底数）

（1）若在其定义域内为单调函数，求的取值范围；

（2）若直线与函数的图象都相切，且与函数的图象相切于点，求的值；

（3）若在上至少存在一点，使得成立，求的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义利用导数研究函数的单调性利用导数求函数的最值利用导数求参数的取值范围

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷