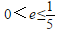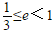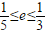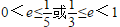- 真题试卷
- 模拟试卷
- 预测试卷
1.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.椭圆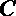
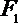
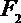
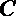
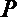
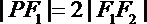
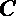
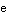
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
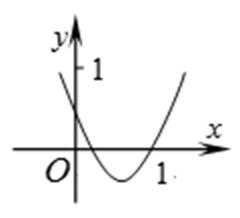
8.下图是二次函数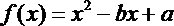
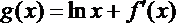
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.如图,执行下边的程序框图,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
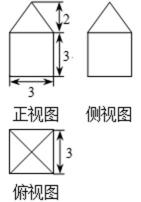
11.一个几何体的三视图如图所示,则此几何体积为________。
正确答案
33
解析
解析已在路上飞奔,马上就到!
知识点
13.过直线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.恬点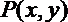
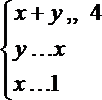
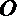
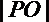
正确答案
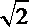
解析
解析已在路上飞奔,马上就到!
知识点
14.若











正确答案
8;5
解析
解析已在路上飞奔,马上就到!
知识点
15.设


(1)求
(2)求


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设

(1)求

(2)求函数

正确答案
(1)由于第一次抛掷骰子的每一个结果都可以与第二次抛掷骰子的任意个结果配对,组成先后抛掷一枚骰子的一个结果,因此先后抛掷一枚骰子的结果共有36种.
其中第一个数表示第一次抛掷骰子的结果,第二个数表示第二次抛掷骰子的结果.因此


(2)函数

则
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,





(1)求证:

(2)求证:
(3)若


正确答案
(1)取
(2)
(3)
解析
解析已在路上飞奔,马上就到!
知识点
19.已知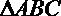
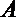
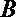
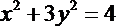
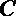
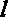
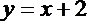
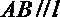
(1)当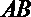
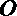
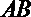
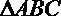
(2)当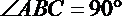
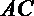
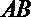
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设
(1)若


(2)当

(3)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.对于给定数列






(1)若







(2)若数列


①求数列
②已知数列


正确答案
解析
解析已在路上飞奔,马上就到!