- 真题试卷
- 模拟试卷
- 预测试卷
5.已知a∈(π,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数y=
正确答案
解析
∵f(﹣x)=﹣f(x)是奇函数,所以排除A,B。当x=1时,f(x)=0排除C,故选D
知识点
10.设α、β都是锐角,且cosα=

正确答案
解析
∵ α、β都是锐角,且cosα=

∴ 



∴ 
∴ cos(α+β)=﹣



则cosβ=cos[(α+β)﹣α]=cos(α+β)cosα+sin(α+β)sinα=﹣




故选A
知识点
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数f(x)=x3+ax2+3x﹣9,已知f(x)在x=-3时取得极值,则a等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.将函数y=2sinx图象上的所有点的横坐标缩小到原来的

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知数列{an}满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知二次函数f(x)的图象如图所示,则其导函数f′(x)的图象大致形状是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.公差不为零的等差数列{an}中,a1+a2+a5=13,且a1、a2、a5成等比数列,则数列{an}的公差等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知a=20.2,b=0.40.2,c=0.40.6,则( )
正确答案
解析
考查指数函数y=0.4x,函数为减函数,∵0.2<0.6,∴0.40.2>0.40.6,∴b>c。考查幂函数y=x0.2,函数为增函数,∵ 2>0.4,∴ 20.2>0.40.2,∴ a>b ∴ a>b>c。故选A.
知识点
14.有下面四个判断:
①命题“设a、b∈R,若a+b≠6,则a≠3或b≠3”是一个假命题;
②若“p或q”为真命题,则p、q均为真命题;
③命题“∀a、b∈R,a2+b2≥2(a﹣b﹣1)”的否定是“∃a、b∈R,a2+b2≤2(a﹣b﹣1)”;
④若函数
其中正确的有
正确答案
④
解析
①当a=3且b=3时,a+b=6,所以命题正确,根据逆否命题和原命题的等价性可知,若a+b≠6,则a≠3或b≠3”为真命题,∴ ①错误.
②若“p或q”为真命题,则p、q至少有一个为真命题,∴ ②错误.
③根据全称命题的否定是特称命题,∴命题“∀a、b∈R,a2+b2≥2(a﹣b﹣1)”的否定是“∃a、b∈R,a2+b2<2(a﹣b﹣1)”,∴ ③错误.
④若函数
故答案为:④.
知识点
15.已知函数
①若x>1,则f(x)>1;
②若0<x1<x2,则f(x2)﹣f(x1)>x2﹣x1;
③若0<x1<x2,则x2f(x1)<x1f(x2);
④若0<x1<x2,则
其中,所有正确命题的序号是
正确答案
①④
解析
①由于x>1,则
②若令x1=1,x2=2,满足0<x1<x2,但f(x2)﹣f(x1)=
③若令x1=1,x2=2,满足0<x1<x2,但x2f(x1)=2>x1f(x2)=
④函数图象如图中所示,对于0<x1<x2,则A、B两点的纵坐标分别为


故答案为①④.
知识点
11.函数f(x)=f′(


正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
12.已知等比数列{an}为递增数列,且a3+a7=3,a2•a8=2,则

正确答案
2
解析
∵ 等比数列{an}为递增数列,a3+a7=3,a2•a8=2,
∴ 
∴ 

∴ q4=2.
∴ 

故答案:2.
知识点
13.已知△ABC的三边分别是a、b、c,且面积

正确答案
45°
解析
由题意,
∵ 
∵ C是△ ABC的内角
∴ C=45°,
故答案为:45°
知识点
16.设函数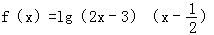
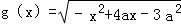
(1)当a=1时,求集合A∩B;
(2)若A∩B=B,求实数a的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知等比数列{an}中,a1=

(I)Sn为{an}的前n项和,证明:Sn=
(II)设bn=log3a1+log3a2+…+log3an,求数列{bn}的通项公式.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.
(1)写出直线l的方程;
(2)求x1x2与y1y2的值;
(3)求证:OM⊥ ON.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(1)求m的值,并求f(x)的单调递增区间;
(2)在△ABC中,角A、B、C的对边a、b、c,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设a是实数,f(x)=a﹣
(1)证明:对于任意实数a,f(x)在R上为增函数;
(2)如果f(x)为奇函数,试确定a的值.
(3)当f(x)为奇函数时,求f(x)的值域.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数
(Ⅰ )当a=1时,求曲线f(x)在x=1处的切线方程;
(Ⅱ )当
(Ⅲ )在(Ⅱ)的条件下,设函数
正确答案
解析
解析已在路上飞奔,马上就到!