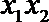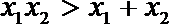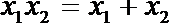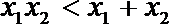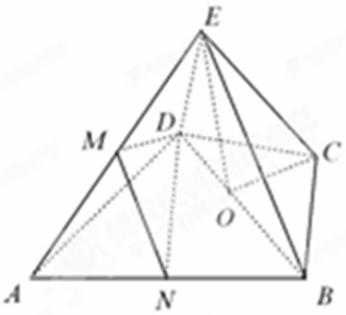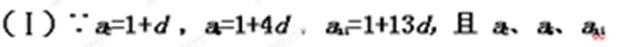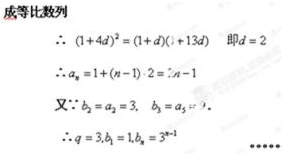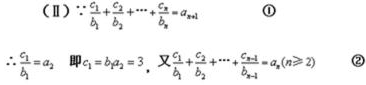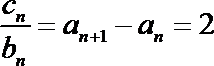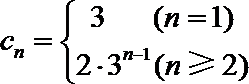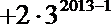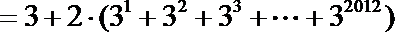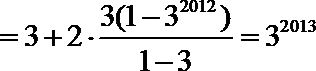- 真题试卷
- 模拟试卷
- 预测试卷
2.下列命题中,真命题是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知命题

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
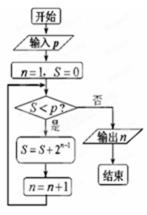
4. 执行右图的程序框图,若输出的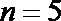
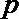
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数y=f(x)是定义在实数集R上的函数,那么y=-f(x+2) 与y=f(6-x)的图象( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.二次函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知椭圆





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数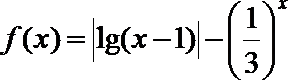
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在三角形ABC中,已知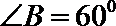
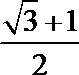
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.几何体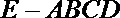
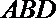
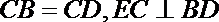
(1)求证:
(2)若∠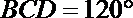
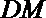
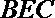
正确答案
(1)设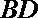
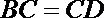
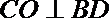
又已知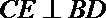
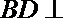
所以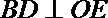
所以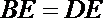
(2)取AB中点N,连接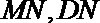
∵M是AE的中点,∴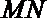
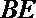
∵△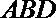
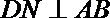
由∠BCD=120°知,∠CBD=30°,所以∠ABC=60°+30°=90°,即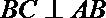
所以ND∥BC,
所以平面MND∥平面BEC,故DM∥平面BEC.
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)求k的值;
(2)求
(3)设



正确答案
(1)

(2)由(I)知,
设



由



当


综上可知,

(3)由(II)可知,∴











解析
解析已在路上飞奔,马上就到!
知识点
17.已知等差数列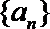
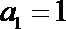
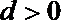
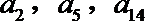
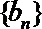
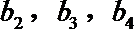
(Ⅰ)求数列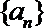
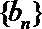
(Ⅱ)设数列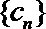
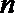
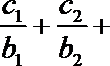
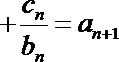
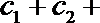
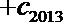
正确答案
①-②:
∴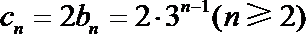
∴
则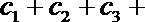

解析
解析已在路上飞奔,马上就到!
知识点
20.已知圆




(1)求m的值及椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求
正确答案
(1)因为直线
所以圆心

即

又因为直线
则左焦点F1的坐标为

所以

解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22,23,24题中任选一题做答。
22.选修4-1:几何证明选讲.
如图,⊙O内切△ABC的边于D、E、F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.
(1)证明:圆心O在直线AD上;
(2)证明:点C是线段GD的中点.
23.选修4-4:坐标系与参数方程选讲.
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为
(1)求圆C的极坐标方程;
(2)



24.选修4-5:不等式选讲.
已知函数
(1)解不等式
(2)若不等式

正确答案
24.(1)根据条件
当
当
当
综上,


(2)由于


又不等式

解析
解析已在路上飞奔,马上就到!
知识点
18.从某学校的










(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的


(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他 们的身高分别为





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球的体积为_______________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知复数z1=a+bi,z2=1+ai(a,b∈R),若|z1|<z2,则b的取值范围是________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,三边a、b、c成等差数列,且B=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.不等式组

正确答案
1
解析
解析已在路上飞奔,马上就到!