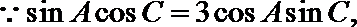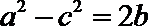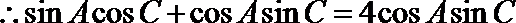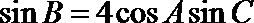文科数学浦东新区2010年高三试卷

精品

填空题
单选题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、填空题

2、单选题

3、简答题

真题试卷
模拟试卷
预测试卷

填空题本大题共14小题，每小题4分，共56分。把答案填写在题中横线上。

题型：填空题

分值: 4分

1．设集合，则__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数单调性的应用

题型：填空题

分值: 4分

2．函数的值域为 ___________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

变化的快慢与变化率

题型：填空题

分值: 4分

7．已知为等差数列，++=105，=99，以表示的前项和，则使得达到最大值的是________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断

题型：填空题

分值: 4分

3．函数的单调递减区间是_____________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：填空题

分值: 4分

4．已知中，的对边分别为，若且，则________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数单调性的应用

题型：填空题

分值: 4分

6．已知等比数列满足，且，则当时，__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：填空题

分值: 4分

5．如果函数的图像关于点中心对称，那么的最小值为_______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

9．某公司一年购买某种货物400吨，每次都购买吨，运费为4万元/次，一年的总存储费用为万元，要使一年的总运费与总存储费用之和最小，则 _________ 吨．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

分值: 4分

8．已知数列满足：则___________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的单调性

题型：填空题

分值: 4分

10．当，不等式成立，则实数的取值范围是__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

12．已知函数.项数为27的等差数列满足，且公差.若，则当=______时，.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

13．对于各数互不相等的整数数组（n是不小于2的正整数），如果在时，有，则称与是该数组的一个“逆序”，一个数组中所有“逆序”的个数称为该数组的“逆序数”。例如，数组（2，4，3，1）中有逆序“2，1”，“4，3”，“4，1”，“3，1”，其“逆序数”等于4。若各数互不相等的正整数数组的“逆序数”是2，则的“逆序数”至少是____________ .

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

11．设是公比为的等比数列，，令，若数列有连续四项在集合中，则=__________

正确答案

-9

解析

解析已在路上飞奔，马上就到！

知识点

求非线性目标函数的最值

题型：填空题

分值: 4分

14．设［x］表示不超过x的最大整数（如［2］=2，［］=1），对于给定的nN*，定义x，则当x时，函数的值域是 ______________________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

单选题本大题共4小题，每小题4分，共16分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 4分

15．“”是“A=30º”的（）

A充分而不必要条件

B必要而不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 4分

16．下图给出的是计算的值的一个程序框图，其中判断框内应填入的条件是（）

Ai＞49

Bi＞50

Ci＞51

Di＞52

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 4分

17．设函数在（，+）内有定义。对于给定的正数K，定义函数：，取函数=。若对任意的，恒有=，则（）

AK的最大值为2

BK的最小值为2

CK的最大值为1

DK的最小值为1

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

分值: 4分

18．如图所示，一质点在平面上沿曲线运动，速度大小不变，其在轴上的投影点的运动速度的图象大致为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

简答题（综合题）本大题共78分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 14分

19．设函数，

（1）求函数的最大值和最小正周期；

（2）解三角方程：.

正确答案

（1）f(x)=cos(2x+)+sinx.

所以函数f(x)的最大值为,最小正周期.

（2）由，

得到 =0

即，

得，

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 14分

20．在中，内角A．B．C的对边长分别为．．，已知，且求b.

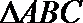
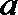
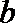
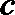
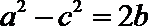
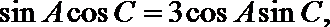
正确答案

解法一：在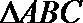中

则由正弦定理及余弦定理有:

a·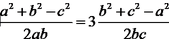·c

化简并整理得：.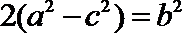

又由已知.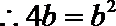

解得.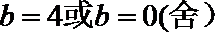

解法二:由余弦定理得:

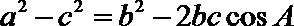
又,，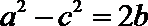

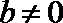
所以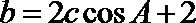……①

又，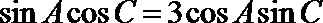

，

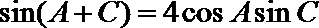
即

由正弦定理得，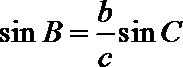

故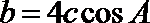……………②

由①，②解得.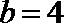

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：简答题

分值: 16分

21．设，函数的定义域为，且，对定义域内任意的，满足，求：

（1）及的值；

（2）函数的单调递增区间。

正确答案

（1）

又：

（2）由（1）知：

又

的增区间为

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 16分

22．设数列的前n项和为对任意的正整数n，都有成立，记，

（Ⅰ）求数列与数列的通项公式；

（Ⅱ）证明：（k为正整数）；

（Ⅲ）设数列的前n项和为R，是否存在正整数k，使得成立？若存在，找出一个正整数k；若不存在，请说明理由.

正确答案

（Ⅰ）当时，。

又∵

∴，即，

∴数列成等比数列，其首项

∴，

（II）证明：由（I）知

（Ⅲ）不存在正整数，使得成立。证明如下：

∴当n为偶数时，设

∴

当n为奇数时，设

∴

∴对于一切的正整数n，都有

∴不存在正整数，使得成立。

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 18分

23．设数列的通项公式为. 数列定义如下：对于正整数m，是使得不等式成立的所有n中的最小值.

（Ⅰ）若，求；

（Ⅱ）若，求数列的前2m项和公式；

（Ⅲ）若，是否存在q，使得？如果存在，求q的取值范围；如果不存在，请说明理由.

正确答案

（Ⅰ）由题意，得，

解，

得.

∴成立的所有n中的最小整数为7，

即.

（Ⅱ）由题意，得，对于正整数，

由，得.

根据的定义可知，当时，；

当时，.

∴

（Ⅲ）假设存在p和q满足条件，

由不等式及得.

∵，

根据的定义可知，

对于任意的正整数m 都有

，

即对任意的正整数m都成立.

当（或）时，

得（或），这与上述结论矛盾！

当，即时，

得，

解得.

∴ 存在p和q，使得；

p和q的取值范围分别是，

解析

解析已在路上飞奔，马上就到！

知识点

不等式的实际应用

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷