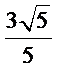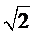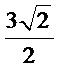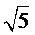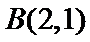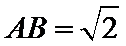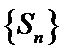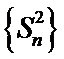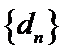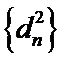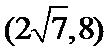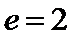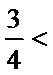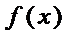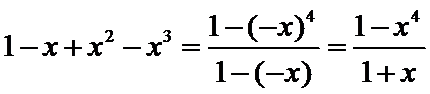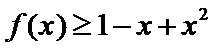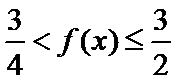- 真题试卷
- 模拟试卷
- 预测试卷
2. 已知互相垂直的平面
正确答案
解析
由题意知

考查方向
解题思路
利用面面垂直求出线线垂直即可
易错点
对直线与平面位置理解不够出现错误
知识点
4. 若平面区域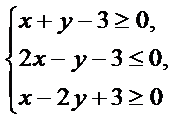
正确答案
解析
画出不等式组的平面区域如题所示,由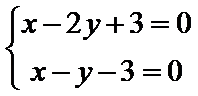
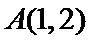
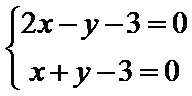
由题意知,当斜率为1的两条直线分别过点A和点B时,两直线的距离最小,即
考查方向
解题思路
画出可行域,利用垂直性质和两点间距离公式求出
易错点
对可行性区域的划分出现错误
知识点
5. 已知a,b>0,且a≠1,b≠1,若
正确答案
解析

当



当



考查方向
解题思路
分类讨论底数的范围,求出范围
易错点
对数函数的性质理解不够
知识点
7. 已知函数


正确答案
解析
试题分析:由已知可设






考查方向
解题思路
利用函数的奇偶性、单调性求出变量的取值范围即可
易错点
对函数的奇偶性、单调性的应用理解不够
知识点
1.已知全集U={1,2,3,4,5,6},集合P={1,3,5},Q={1,2,4},则
正确答案
解析
根据补集的运算,得
考查方向
解题思路
求补集的运算和并的运算即可
易错点
对补集的运算和并的运算出现错误
知识点
3. 函数y=sinx2的图象是( )
正确答案
解析
因为




考查方向
解题思路
求函数的特殊值即可,利用排除法
易错点
对函数图像的特殊值取法理解不够出现错误
知识点
6. 已知函数f(x)=x2+bx,则“b<0”是“f(f(x))的最小值与f(x)的最小值相等”的( )
正确答案
解析
由题意知
令

当



反之则不能成立
考查方向
解题思路
利用函数的最值求出a的范围,既而利用条件求出即可
易错点
对函数最值问题和条件满足条件理解不够
知识点
8. 如图,点列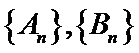
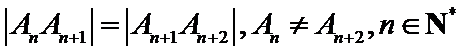
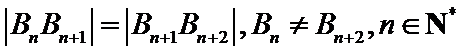
(P≠Q表示点P与Q不重合)
若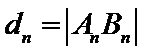
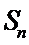
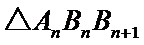
正确答案
解析
试题分析: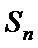
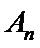
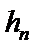
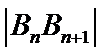
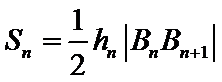
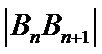
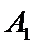
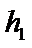
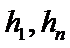
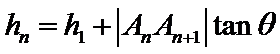
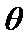
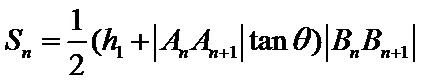
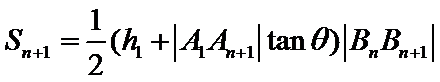
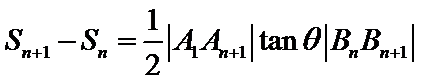
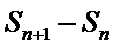
考查方向
解题思路
求出三角形的高、再求出三角形面积求出关系式,再根据关系式得出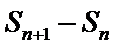
易错点
对定义题的创新题理解不够、三角形面积表示困难
知识点
9. 某几何体的三视图如图所示(单位:cm),则该几何体的表面积是______cm2,体积是______cm3.
正确答案
80 ;40.
考查方向
解题思路
先画出立体几何体,再求出图形的表面积和体积
试题分析:由三视图知该组合体是一个长方体上面放置了一个小正方体,

易错点
对三视图变成立体几何体存在问题
知识点
10. 已知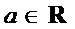
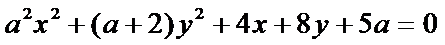
正确答案
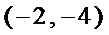
解析
试题分析:由题意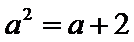
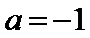
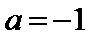

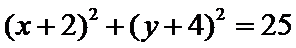
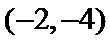
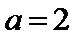
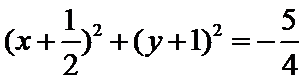
考查方向
解题思路
先由题意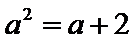
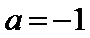
易错点
对圆的标准方程理解不够
知识点
13.设双曲线x2–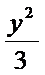
正确答案
解析
由已知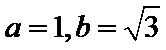
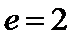
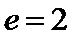
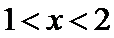
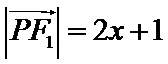
由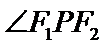
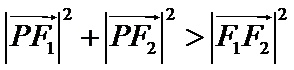
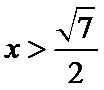
考查方向
解题思路
先由题意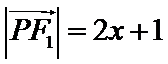
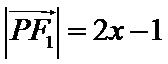
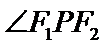
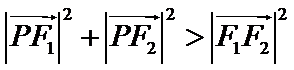
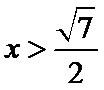
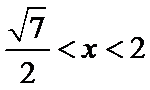
易错点
对双曲线的几何性质、锐角三角形的条件不熟悉,计算错误
知识点
14.如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD=
正确答案
解析
设直线AC与
设O为AC中点,由已知得





考查方向
解题思路
先由题意设直线AC与


求出即可
易错点
对异面直线所成角、最值问题不熟悉,计算错误
知识点
15.已知平面向量a,b,|a|=1,|b|=2,a·b=1.若e为平面单位向量,则|a·e|+|b·e|的最大值是______.
正确答案
解析
由已知得

考查方向
解题思路
先由题意由已知得


易错点
对平面向量的数量积和模知识不熟悉,计算错误
知识点
11. 已知
正确答案

解析

考查方向
解题思路
先由题意
易错点
对三角函数的三角恒等变换不熟悉,计算错误
知识点
12.设函数f(x)=x3+3x2+1.已知a≠0,且f(x)–f(a)=(x–b)(x–a)2,x∈R,则实数a=_____,b=______.
正确答案
-2;1.
解析
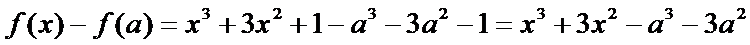
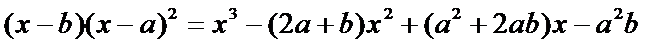
所以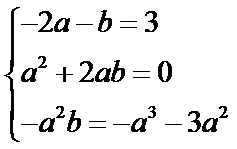
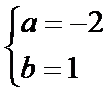
考查方向
解题思路
先由题意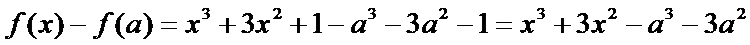
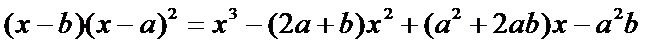
易错点
对函数解析式的求法不熟悉,计算错误
知识点
设数列{






18.求通项公式
19.求数列{

正确答案

解析
由题意得:

又当

得
所以,数列

考查方向
解题思路
先由


正确答案

解析
设


当


设数列



当

所以,
考查方向
解题思路
设



易错点
对等差、等比数列的基础知识,同时考查数列基本思想方法等基础知识不熟悉,计算错误
如图,设抛物线
22.求p的值;
23.若直线AF交抛物线于另一点B,过B与x轴平行的直线和过F与AB垂直的直线交于点N,AN与x轴交于点M.求M的横坐标的取值范围。
正确答案
p=2
解析
由题意可得抛物线上点A到焦点F的距离等于点A到直线x=-1的距离.
由抛物线的定义得,即p=2
考查方向
解题思路
由抛物线定义求出p=2.
易错点
对抛物线的几何性质、直线与抛物线的位置关系等基础知识不熟悉,计算错误
正确答案

解析
抛物线的方程为


因为AF不垂直于y轴,可设直线AF:x=sy+1,




又直线AB的斜率为

从而的直线FN:

所以
设M(m,0),由A,M,N三点共线得:
于是
综上,点M的横坐标的取值范围是
考查方向
解题思路
设直线AF:x=sy+1,求出



易错点
对抛物线的几何性质、直线与抛物线的位置关系等基础知识不熟悉,计算错误
设函数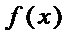
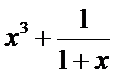
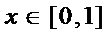
24.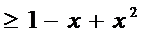
25.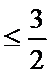
正确答案
证明详见解析
解析
(Ⅰ)因为
由于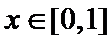
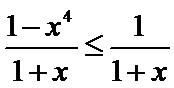
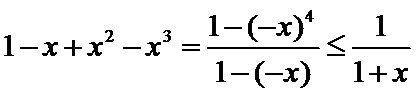
所以
考查方向
解题思路
利用放缩法,得到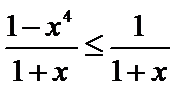
易错点
对函数的单调性与最值、分段函数等基础知识不熟悉,计算错误
正确答案
证明详见解析.
解析
由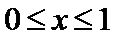
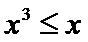
故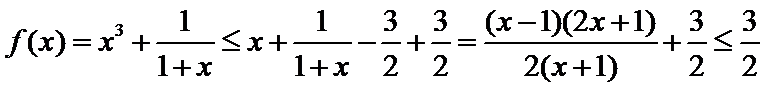
所以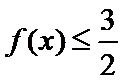
由(Ⅰ)得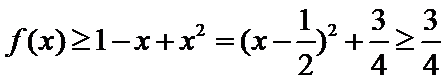
又因为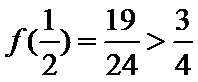
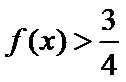
综上,
考查方向
解题思路
由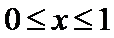
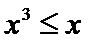
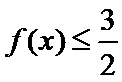
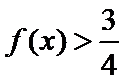
易错点
对函数的单调性与最值、分段函数等基础知识不熟悉,计算错误
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b+c=2acos B.
16.证明:A=2B;
17.若cos B=
正确答案


解析
由正弦定理得
故
于是,
又



因此,

所以,
考查方向
解题思路
先由正弦定理得

易错点
对三角函数及其变换、正弦和余弦定理等基础知识不熟悉,计算错误
正确答案

解析
由


故


考查方向
解题思路
由




易错点
对三角函数及其变换、正弦和余弦定理等基础知识不熟悉,计算错误
如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
20.求证:BF⊥平面ACFD;
21.求直线BD与平面ACFD所成角的余弦值.
正确答案
证明详见解析
考查方向
解题思路
先延长





因为平面




又因为


所以
易错点
对空间点、线、面位置关系、线面角等基础知识不熟悉,计算错误
正确答案

解析
因为
所以
在


所以直线BD与平面ACFD所成的角的余弦值为
考查方向
解题思路


易错点
对空间点、线、面位置关系、线面角等基础知识不熟悉,计算错误
“计数原理与概率”模块(10分)
28.已知(1+2x)4(1-x2)3=a0+a1x+a2x2+…a10x10,求a2的值
29.设袋中共有8个球,其中3个白球、5个红球,从袋中随机取出3个球,求至少有1个白球的概率
正确答案
因为( 1+2x)4二项展开式的通项为
( 1一x2 )3二项展开式的通项为
所以
正确答案
从袋中取出3个球,总的取法有 C83=56种;
其中都是红球的取法有 C53 = 10种.
因此,从袋中取出3个球至少有1个白球的概率是
自选模块数学试题
“复数与导数”模块(10分)
26.已知i为虚数单位,若复数z满足(z+i)2=2i,求复数z
27.求曲线y=2x2+lnx在点(1,2)处得切线方程。
正确答案
设复数z=a+bi,a,b∈ R,由题意得
a2—(b十1)2十2a(b十1)i=2i,
解得
正确答案
由于