- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.运行下图所示框图的相应程序,若输入



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知命题




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若直线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知直线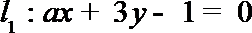
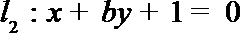
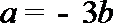
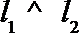
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如图所示,三棱锥







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.如图,已知P是边长为2的正三角形的边BC上的动点,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,在等腰梯形













正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设双曲线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.过抛物线








正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
14.路灯距地平面为8m,一个身高为1.75m的人以

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数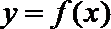
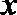
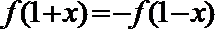
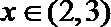
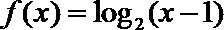
① 函数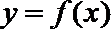
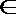
② 函数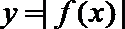
③ 当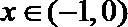
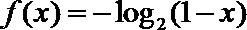
④ 函数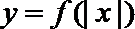
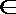
其中所有正确结论的序号为
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
16. 某品牌汽车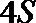
已知分3期付款的频率为0.2,该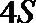
(Ⅰ)求上表中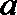
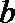
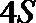
(Ⅱ)该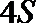
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.函数 

(Ⅰ)求
(Ⅱ)设锐角△ABC的内角A、B、C所对的边分别为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知单调递增的等比数列{aBnB}满足:aB2B+aB3B+aB4B=28,且aB3B+2是aB2B,aB4B的等差中项.
(Ⅰ)求数列{aBnB}的通项公式;
(Ⅱ)若

值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.一个四棱锥的三视图和直观图如图所示,其中俯视图中
(Ⅰ)求证:PB//平面AEC;
(Ⅱ)若F为侧棱PA上的一点,且


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 设函数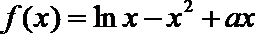
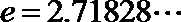
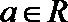
(Ⅰ)当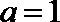
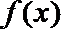
(Ⅱ)若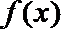
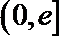
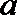
(Ⅲ)设函数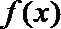
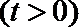
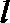
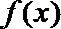
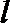
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知抛物线



(1)求抛物线

(2)过点







(3)直线













正确答案
解析
解析已在路上飞奔,马上就到!