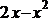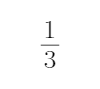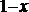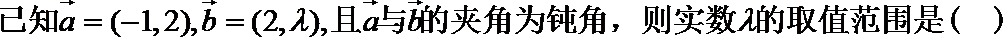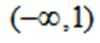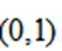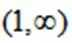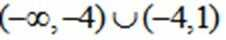- 真题试卷
- 模拟试卷
- 预测试卷
3.下列函数中,在区间(0,1)上为减函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知|





正确答案
解析
解析已在路上飞奔,马上就到!
知识点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知向量→OA=(4,6),→OB=(3,5),且→OC⊥→OA,→AC∥→OB,则向量→OC= ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 函数f(x)=1+log2x 与g(x)=2
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知命题p: 

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在△ABC中,“A>300”是“sinA> ”的( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.等差数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.各项均为正数的等比数列{an}的前n项和为Sn,若Sn=2 ,S3n=14,则S4n等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若cos(α+β)=,cos(α-β)=,则tanα·tanβ=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设{an}是公比q>1的等比数列,若a2008和a2009是方程4x2-8x+3=0的两根,则a2009+a2010=( )
正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
15.幂函数f(x)=x
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
16.一分组数列如下表
现用ai,j表示第i行的第j个数,求a2n,1=( )
正确答案
2n—2行共
解析
解析已在路上飞奔,马上就到!
知识点
18.已知二次函数f(x)=x2-4ax+2a+6 (a∈R)
(1)若对x∈R,都有f(2-x)=f(2+x),求函数f(x)在[0,3]上的最小值和最大值;
(2)若函数f(x)的值域为[0,+∞),且a>0,求函数g(x)=loga(x2-2x-3)的减区间。
正确答案
(1)∵f(2-x)=f(2+x),
∴f(x)的图象关于直线x=2对称
∴2a=2,∴a=1 ,
∴f(x)=(x-2)2+4 ,
∵x∈[0,3],
∴当x=2时,fmin(x)=f(2)=4
当x=0时,fmax(x)=f(0)=8
(2)若f(x)的值域为[0,+∞),则 -4a2+2a+6=0,∵a>0,
∴g(x)=log
∴g(x)的减区间为(-∞,-1) .
解析
解析已在路上飞奔,马上就到!
知识点
20.在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c =
(1) 求角C的大小; (2)求△ABC的面积。
正确答案
(2)由余弦定理得:c2=a2+b2-2abcosC,即7=a2+b2-ab
∴
由条件a+b=5得 7=25-3ab
∴
解析
解析已在路上飞奔,马上就到!
知识点
17.数列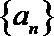
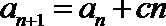


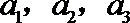

(I)求
(II)求
正确答案
答案:(I)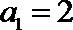
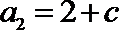

因为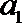
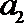
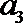
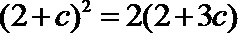
解得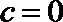
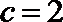
当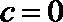
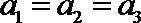
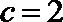
(II)当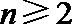
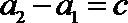

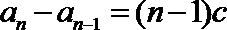
所以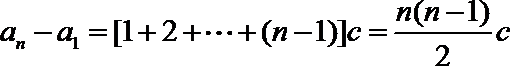
又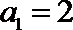
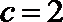
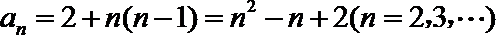
当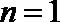
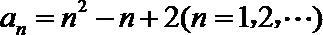
解析
解析已在路上飞奔,马上就到!
知识点
19.已知向量


(1)求

(2)若

正确答案
(1)∵



代入

又
(2)∵



∴
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数
(1)求函数
(2)若关于



正确答案
(1)函数

∵
∵





(2)方法1:∵
∴
令


由



故

即

综上所述,

方法2:∵
∴
即

∵


∴


∵



故


即
综上所述,

解析
解析已在路上飞奔,马上就到!
知识点
22.已知数列







(1)求数列
(2)设




正确答案
(2)∵


∴
∴
∴
(ⅰ)当

当且仅当

∴
(ⅱ)当

当且仅当


∴
即


综上所述,存在


解析
解析已在路上飞奔,马上就到!