文科数学海淀区2015年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共8小题，每小题5分，共40分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．已知集合，，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

3．若且，函数的反函数图像一定过点，则的坐标是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

4．已知A ，B，C三点不重合，则“”是“A，B，C三点共线”成立的（）

A充分不必要条件

B必要不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

8．在股票买卖过程中，经常用到两种曲线，一种是即时价格曲线y＝f(x)，一种是平均价格曲线y＝g(x) ，( 如f(2)＝3表示开始交易后第2小时的即时价格为3元；g(2)＝4表示开始交易后两个小时内所有成交股票的平均价格为4元 ).下面所给出的四个图象中，实线表示y＝f(x)，虚线表示y＝g(x)，其中可能正确的是( )

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

2．函数图像的一个对称中心为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

6．若实数满足则的最小值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：单选题

分值: 5分

7．若曲线上有且只有一个点到其焦点的距离为1，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的标准方程和几何性质

题型：单选题

分值: 5分

5．设为两条直线，为两个平面，下列四个命题中，正确的命题是（）

A若与所成的角相等，则

B若，，，则

C若，，，则

D若，，，则

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

填空题本大题共6小题，每小题5分，共30分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11．在△ABC中，AC=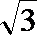，∠A=45°，∠C=75°，则BC的长为___________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：填空题

分值: 5分

9．函数的定义域是___________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

12．已知圆：内有一点，直线过点交圆于两点，若为中点，则__________;若，则的方程为__________。

正确答案

；

解析

解析已在路上飞奔，马上就到！

知识点

圆的标准方程

题型：填空题

分值: 5分

14．定义一个对应法则．现有点与，点是线段上一动点，按定义的对应法则．若点M坐标为（4，4），则对应点的坐标为__________；当点在线段上从点开始运动到点结束时，点的对应点所经过的路线长度为___________．

正确答案

；

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

13．已知等差数列的首项及公差d都是整数，前n项和为（）.若，则通项公式

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：填空题

分值: 5分

10．展开式中第5项为常数项，则正整数的值是___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

简答题（综合题）本大题共80分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

15．已知函数f(x)＝2sinxcosx＋cos2x.

（Ⅰ）求f ()的值；

（Ⅱ）设∈(0，)，f ()＝，求cos2的值。

正确答案

（Ⅰ）∵f(x)=sin2x+cos2x,

∴f()=sin+cos=1

（Ⅱ）∵f()=sinα+cosα=,

∴1+sin2α=, sin2α=,

∴ cos2α=∵α∈（0，π）

∴2α∈（π，π） ∴cos2α<0.

故cos2α=

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 13分

16．在一次百米比赛中，甲，乙等6名同学采用随机抽签的方式决定各自的跑道，跑道编号为1至6，每人一条跑道

（1）求甲在1或2 跑道且乙不在5或6跑道的概率；

（2）求甲乙之间恰好间隔两人的概率。

正确答案

（1）

（2）（总数为，间隔2人有三种可能，如1且4跑道，故
）

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：简答题

分值: 14分

17．如图，在四棱柱ABCD-中，AB=BC=CA=，AD=CD==1,

平面，

（Ⅰ）

（Ⅱ）

（Ⅲ）若，所成角大小

正确答案

（Ⅰ）证：在四棱锥中，

，且，

取中点，则

三点在一条直线上。

又面面

面面，

面，，

面，

；

（Ⅱ）连，在中

在正中，，

又在正中，，

∴，

又面，面，

面，

在四棱锥中，，面，面，

∴// 面，

又，

∴面面，

又面，故面。

（Ⅲ）过作的垂线，设垂足为，面面，

面，

连，则为在面内的射影，

所以为直线与面所成角，

由已知得：。

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 14分

18．数列的前项和记为

（Ⅰ）求的通项公式；

（Ⅱ）等差数列的各项为正，其前项和为，且，又成等比数列，求

（Ⅲ）设，在（II）的条件下，设，求的最小值。

正确答案

（Ⅰ）由可得，

两式相减得

又 ∴

故是首项为，公比为得等比数列

∴

（Ⅱ）设的公比为

由得，可得，可得

故可设

又

由题意可得

解得

∵等差数列的各项为正，∴

∴

（Ⅲ）由已知得：，对称轴，

，

①若，则，此时最小值为；

②若，此时最小值为；

③若，此时最小值为。

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 13分

19．设椭圆的左、右焦点分别是F1和F2 ，离心率，点F2到右准线的距离为.

（1）求的值；

（2）设M、N是右准线上两动点，满足当取最小值时，求证：M，N两点关于轴对称

正确答案

（1）因为,F2到l的距离,

所以由题设得

解得

由

(Ⅱ)由,a=2得l的方程为.

故可设

由知

得 ,所以y1y20,,

当且仅当时，上式取等号，此时。

即M，N两点关于轴对称

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：简答题

分值: 14分

20．已知函数的图象经过原点，且在x=1处取得极大值。

（Ⅰ）求实数的取值范围；

（Ⅱ）若方程恰好有两个不同的根，求的解析式；

（Ⅲ）对于（2）中的函数，若对于任意实数α和β恒有不等式成立，求m的最小值.

正确答案

（Ⅰ），，

，

由或

因为当时取得极大值，所以，

所以的取值范围是：；

（Ⅱ）由下表：

画出的简图：

依题意得：，

解得：，

所以函数的解析式是：

；

（Ⅲ）对任意的实数都有，

依题意有：函数在区间上的最大值与最小值的差不大于，

在区间上有：,

的最大值是，的最小值是，

所以即的最小值是。

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷