- 真题试卷
- 模拟试卷
- 预测试卷
2.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.如果


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若函数

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
7.把



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设


正确答案
-3
解析
解析已在路上飞奔,马上就到!
知识点
3.在二项式

正确答案
-5
解析
解析已在路上飞奔,马上就到!
知识点
5.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图,在平行四边形



正确答案
18
解析
解析已在路上飞奔,马上就到!
知识点
9.已知命题“任意


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数










正确答案
④
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若函数




正确答案
10
解析
解析已在路上飞奔,马上就到!
知识点
14.设函数




正确答案
[-3,6]
解析
解析已在路上飞奔,马上就到!
知识点
18.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.从






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在空间四边形











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数



(1)试确定
(2)若不等式


正确答案
(1)∵f(x)=b·ax的图象过点A(1,6),B(3,24)
∴
②÷①得a2=4,又a>0,且a≠1,
∴a=2,b=3,∴f(x)=3·2x.
(2) 
化为
令
∴m≤g(x)min=g(1)=
故所求实数m的取值范围是
解析
解析已在路上飞奔,马上就到!
知识点
20.在



(1)求
(2)若

正确答案
(1)因为

又
=


(2)由已知得
因为

又因为
所以


此时
所以

解析
解析已在路上飞奔,马上就到!
知识点
21.如图,在四棱锥









(1)证明:直线
(2)求异面直线

正确答案
方法一(综合法)
(1)取OB中点E,连接ME,NE
又
(2)



连接

所以 

方法二(向量法)作
如图,分别以AB,AP,AO所在直线为

(1)
设平面OCD的法向量为

即

(2)设





解析
解析已在路上飞奔,马上就到!
知识点
22.已知焦点在





(1)求椭圆
(2)已知过点







正确答案
(1)设椭圆

且
由题意可知:
所以
所以,椭圆

(2)当直线

直线

由
解得:
即


则直线



因为 
所以 
所以 
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列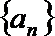
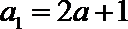
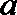
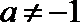
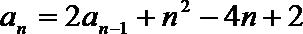
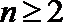
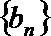
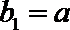
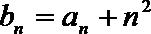
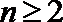
(1)证明: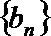
(2)设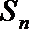
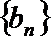
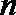
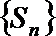
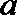
(3)当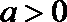
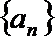
正确答案
(1)∵
∴
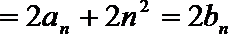
由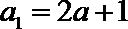
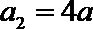
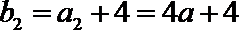
∵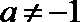
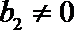
即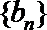
(2)
当n≥2时,
∵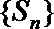
∴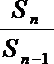
∴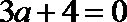
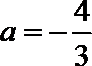
(3)由(1)知当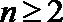
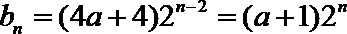
所以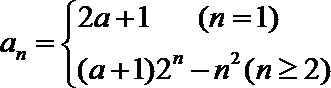
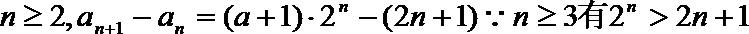
显然最小项是前三项中的一项.
当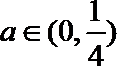
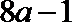
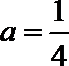
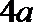
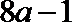
当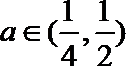
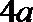
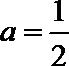
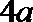
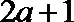
当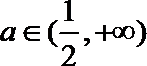
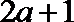
解析
解析已在路上飞奔,马上就到!