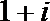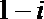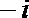- 真题试卷
- 模拟试卷
- 预测试卷
1.设全集


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.一组数据3,4,5,s,t的平均数是4,中位数是m,则过点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.针对近期频繁出现的校车事故,国家决定制定校车标准以保障幼儿园儿童的人生安全,已知某大型公办幼儿园计划用350万元购买A型和B型两款车投入运营,购买总量不超过15辆,其中购买A型校车需25万元/辆,购买B型校车需20万元/辆,假设A型校车的准坐最大人数为30人/辆,B型校车的准坐最大人数为25人/辆,那么为了使该校车所能接送的学生人数最多,则须安排购买( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.给定两个模为1的平面向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知复数Z的实部为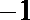
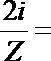
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.从

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知圆

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
12.一支运动队有男运动员56人,女运动员42人,用分层抽样的方法从全体运动员中抽出一个样本,已知某个男运动员被抽中的概率为
正确答案
12
解析
解析已在路上飞奔,马上就到!
知识点
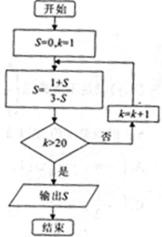
13.如图所示,程序框图的输出结果是__________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.某几何体的三视图如图所示,则该几何体的表面积为__________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.对于函数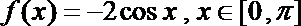
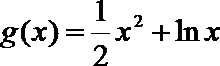
①函数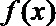
②方程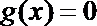
③函数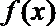
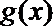
④若函数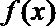
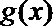
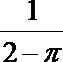
其中正确的是__________(把所有正确命题的序号都填上)
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,ABCD是边长为2的正方形,

(Ⅰ)求证:
(Ⅱ)求证:AC//平面BEF;
(Ⅲ)求几何体EFABCD的体积.
正确答案
解:
(I)证明:∵


∵ABCD是正方形,∴

(II)证明:延长DA,EF相交于点M,连接BM,
∵

又DE=2AF,∴AM=AD=2,

∴AC//MB,
又MB 

∴AC//平面BEF.
(III)由(II)可知几何体EFABCD的体积等于四棱锥

∵




所以几何体EFABCD的体积为
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(Ⅰ)根据表格提供的数据求函数
(Ⅱ)求当

正确答案
解:(Ⅰ)依题意,
又


∴
(Ⅱ)∵
∴
解析
解析已在路上飞奔,马上就到!
知识点
17.为了调查高中学生是否喜欢数学与性别的关系,某班采取分层抽样的方法从2011届高一学生中随机抽出20名学生进行调查,具体情况如下表所示.
(Ⅰ)用独立性检验的方法分析有多大的把握认为本班学生是否喜欢数学与性别有关?
(参考公式和数据:
(1)
(2)①当
②当
③当
④当
(Ⅱ)若按下面的方法从这个20个人中抽取1人来了解有关情况:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号,试求:
①抽到号码是6的倍数的概率;
②抽到“无效序号(序号大于20)”的概率.
正确答案
解:(I)
故有90%以上的把握认为学生选数学与性别有关.
(II)正六面体骰子连续投掷两次,利用列表法可知共有36种情况,抽到号码是6的倍数的有(1,6),(2,3),(2,6),(3,2),(3,4),(3,6),(4,3),(4,6),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)共15种情况. 抽到无效序号有(4,6),(6,4),(5,6),(6,5),(6,6),(5,5),共6种情况.
所以①抽到号码是6的倍数的概率为
②抽到“无效序号”的概率为
解析
解析已在路上飞奔,马上就到!
知识点
19.设函数
(Ⅰ)当

(Ⅱ)令


正确答案
解:(Ⅰ)依题意,知
当
令
当


当


所以

(Ⅱ)
则有
在
当


解析
解析已在路上飞奔,马上就到!
知识点
20.国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费.住宿费及生活费. 每一年度申请总额不超过6000元. 某大学2010届毕业生凌霄在本科期间共申请了24000元助学贷款,并承诺在毕业后3年内(按36个月计)全部还清.
签约的单位提供的工资标准为第一年内每月1500元,第13个月开始,每月工资比前一个月增加5%直到4000元. 凌霄同学计划前12个月每个月还款额为500元,第13个月开始,每月还款额比前一个月多x元.
(Ⅰ)若凌霄恰好在第36个月(即毕业后三年)还清贷款,求x的值;
(Ⅱ)当
正确答案
解:(Ⅰ)依题意,从第13个月开始,每个月的还款额为
其中
从而,到第36个月,凌霄共还款
解得
即要使在三年全部还清,第13个月起每个月必须比上一个月多还20元.
(Ⅱ)设凌霄第n个月还清,则应有:

整理可得
解得

即凌霄工作31个月就可以还清贷款.
解析
解析已在路上飞奔,马上就到!
知识点
21.设






(Ⅰ)求椭圆方程;
(Ⅱ)若直线AB过椭圆的焦点

(Ⅲ)试问
正确答案
解:(Ⅰ)由

(Ⅱ)设AB的方程为


由已知:
解得
(Ⅲ)当A为顶点时,B必为顶点,则
当A.B不为顶点时,设AB方程为y=kx+m,
由


又

∴三角形的面积为定值1
解析
解析已在路上飞奔,马上就到!