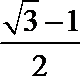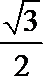- 真题试卷
- 模拟试卷
- 预测试卷
6.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.抛掷两枚质地均匀的骰子,向上的点数之差的绝对值为3的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.执行如图所示的算法,则输出的结果是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.图是某几何体的三视图,则该几何体的体积等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设变量x、y满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在等比数列{an}中,a2a3a7=8,则a4=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设函数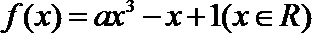


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.椭圆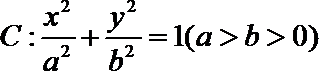
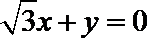
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.过点A(3,1)的直线


正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
16.在三棱锥P-ABC中,PB=6,AC=3,G为△PAC的重心,过点G作三棱锥的一个截面,使截面平行于直线PB和AC,则截面的周长为( ).
正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
13.若复数z满足z=i(2+z)(i为虚数单位),则z=( )
正确答案
-1+i
解析
解析已在路上飞奔,马上就到!
知识点
14.设等差数列{an}的前n项和为Sn,S3 =6,S4=12,则S6= ( ).
正确答案
30
解析
解析已在路上飞奔,马上就到!
知识点
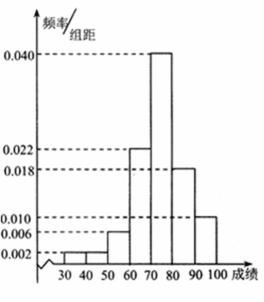
19.为了调查某校学生体质健康达标情况,现采用随机抽样的方法从该校抽取了m名学生进行体育测试.根据体育测试得到了这m名学生各项平均成绩(满分100分),按照以下区间分为七组:[30,40), [40, 50), [50, 60), [60, 70),[70,80),[80,90),[90,100),并得到频率分布直方图(如图),已知测试平均成绩在区间[30,60)有20人.
(I)求m的值及中位数n;
(II)若该校学生测试平均成绩小于n,则学校应适当增加体育活动时间.根据以上抽样调查数据,该校是否需要增加体育活动时间?
正确答案
(I)由频率分布直方图知第1组,第2组和第3组的频率
分别是0.02,0.02和0.06,
则m×(0.02+0.02+0.06)=20,
解得m=200.
由直方图可知,中位数n位于[70,80),则0.02+0.02+0.06+0.22+0.04(n-70)=0.5,
解得n=74.5.
(II)设第i组的频率和频数分别为pi和xi,由图知,
p1=0.02,p2=0.02,p3=0.06,p4=0.22,p5=0.40,p6=0.18,p7=0.10,
则由xi=200×pi,可得
x1=4,x2=4,x3=12,x4=44,x5=80,x6=36,x7=20,
故该校学生测试平均成绩是
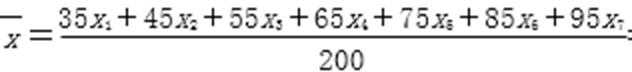
所以学校应该适当增加体育活动时间.
解析
解析已在路上飞奔,马上就到!
知识点
17.在△ABC中,角A,B,C所对的边分别为a,b,c,且csinB=bcos C=3.
(I)求b;
(II)若△ABC的面积为
正确答案
(I)由正弦定理得sinCsinB=sinBcosC,
又sinB≠0,所以sinC=cosC,C=45°.
因为bcosC=3,所以b=3 
(II)因为S=

据余弦定理可得c2=a2+b2-2abcosC=25,所以c=5.
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,∠PCD=90°,PA =AB=AC.
(I)求证:AC⊥CD;
(II)点E在棱PC的中点,求点B到平面EAD的距离.
正确答案
(I)证明:
因为PA⊥ 底面ABCD,所以PA⊥ CD,
因为∠ PCD=90°,所以PC⊥ CD,
所以CD⊥ 平面PAC,
所以CD⊥ AC.
(II)因为PA=AB=AC=2,E为PC的中点,
所以AE⊥ PC,AE=
由(I)知AE⊥ CD,
所以AE⊥ 平面PCD.
作CF⊥ DE,交DE于点F,
则CF⊥ AE,则CF⊥ 平面EAD.
因为BC∥ AD,所以点B与点C到平面EAD的距离相等,
CF即为点C到平面EAD的距离.
在Rt△ ECD中,CF=

所以,点B到平面EAD的距离为
解析
解析已在路上飞奔,马上就到!
知识点
20.已知抛物线y2= 2px(p>0),过点C(一2,0)的直线

(I)求抛物线的方程;
(II)当以AB为直径的圆与y轴相切时,求直线
正确答案
(I)设 l:x=my-2,
代入y2=2px,
得y2-2pmy+4p=0.(*)
设A(x1,y1),B(x2,y2),
则y1+y2=2pm,y1y2=4p,
则x1x2=
因为
所以x1x2+y1y2=12,
即4+4p=12,
得p=2,
抛物线的方程为y2=4x.
(II)由(I)(*)化为y2-4my+8=0.
y1+y2=4m,y1y2=8.
设AB的中点为M,
则|AB|=2xm=x1+x2=m(y1+y2)-4=4m2-4, ①
又|AB|=

由①②得(1+m2)(16m2-32) =(4m2-4)2,
解得m2=3,m=±
所以,直线l的方程为x+

解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22,23,24三题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-1:几何证明选讲
如图,四边形么BDC内接于圆,BD= CD,过C点的圆的切线与AB的延长线交于E点.
(1)求证:∠EAC=2∠DCE;
(2)若BD⊥AB,BC=BE,AE=2,求AB的长.
23.选修4—4;坐标系与参数方程
极坐标系的极点为直角坐标系xOy的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线C的极坐标方程为


(1)求C的直角坐标方程,
(2)直线
24.选修4-5:不等式选讲
设函数
(1)求a;
(2)已知两个正数m,n满足m2+n2=a,求
正确答案
22.(1)证明:因为BD=CD,所以∠BCD=∠CBD.
因为CE是圆的切线,所以∠ECD=∠CBD.
所以∠ECD=∠BCD,所以∠BCE=2∠ECD.
因为∠EAC=∠BCE,所以∠EAC=2∠ECD.
(2)解:因为BD⊥AB,所以AC⊥CD,AC=AB.
因为BC=BE,所以∠BEC=∠BCE=∠EAC,所以AC=EC.
由切割线定理得EC2=AE•BE,即AB2=AE•(AE-AB),即
AB2+2 AB-4=0,解得AB=
23.(1)由ρ=2(cosθ+sinθ),得ρ2=2(ρcosθ+ρsinθ),
即x2+y2=2x+2y,即(x-1) 2+(y-1) 2=2.
l的参数方程为
(2)将
解得,
|EA|+|EB|=| t1|+| t2|=|t1-t2|=
24.(1)
当x∈(-∞,0]时,f(x)单调递减,
当x∈[0,+∞)时,f(x)单调递增,
所以当x=0时,f(x)的最小值a=1.
(2)由(1)知m2+n2=1,由m2+n2≥2mn,得mn≤
则

所以

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数





(1)求a,b的值和直线
(2)证明:除切点外,曲线C1,C2位于直线
正确答案
(1)f'(x)=aex+2x,
g'(x)=cosx+b,
f(0)=a,f'(0)=a,
g(


曲线y=f(x)在点(0,f(0))处的切线为y=ax+a,
曲线y=g(x)在点(

y=b(x-

即y=bx+1.
依题意,有a=b=1,
直线l方程为y=x+1.
(2)由(1)知f(x)=ex+x2,
g(x)=sinx+x.
设F(x)=f(x)-(x+1)=ex+x2-x-1,
则F’(x)=ex+2x-1,
当x∈(-∞,0)时,
F’(x)<F’(0)=0;
当x∈(0,+∞)时,
F’(x)>F’(0)=0.
F(x)在(-∞,0)单调递减,在(0,+∞)单调递增,
故F(x)≥F(0)=0.
设G(x)=x+1-g(x)=1-sinx,
则G(x)≥0,
当且仅当x=2k+
综上可知,f(x)≥x+1≥g(x),
且两个等号不同时成立,因此f(x)>g(x).
所以:除切点外,曲线C1,C2位于直线l的两侧.
解析
解析已在路上飞奔,马上就到!