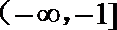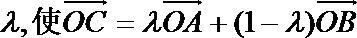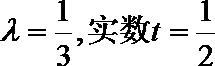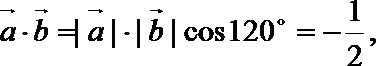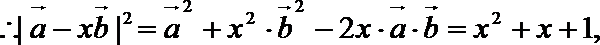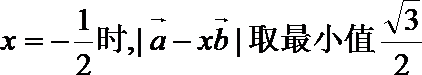- 真题试卷
- 模拟试卷
- 预测试卷
3. “a=1”是函数y=cos2ax－sin2ax的最小正周期为“π”的（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4.已知
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6.已知函数
A（0,
B（0,
C [
D（
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8.在
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7.在∆ABC中，已知D是AB边上一点，若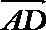
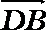
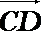
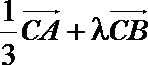
A
B
C-
D-
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10.将函数y＝sinx－cosx的图象沿x轴向右平移a（a>0）个单位长度，所得函数的图象关于y轴对称，则a的最小值是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1.已知集合
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2.复数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5.已知△ABC中，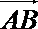
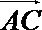
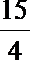
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11.已知
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12.已知函数
A（-∞，0]
B（-∞，1]
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14.已知向量
正确答案
3
解析
解析已在路上飞奔，马上就到！
知识点
13.在等差数列
正确答案
-1
解析
解析已在路上飞奔，马上就到！
知识点
16.若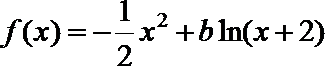
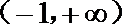
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
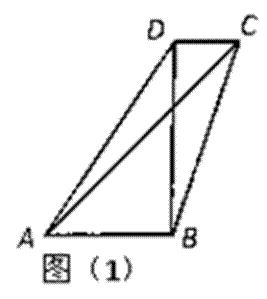
15.如图（1），在四边形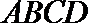
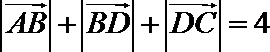
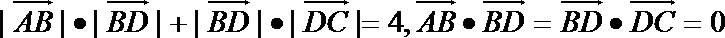
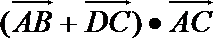
正确答案
4
解析
解析已在路上飞奔，马上就到！
知识点
18.设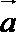
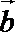
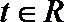
（1）记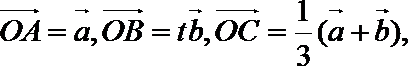
（2）若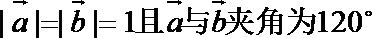
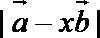
正确答案
解：（1）A、B、C三点共线知存在实数
即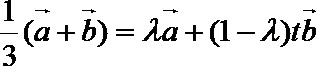
则
（2）
当
解析
解析已在路上飞奔，马上就到！
知识点
17.已知函数
（1）求ω的值；
（2）求f（x）的单调递增区间。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20.数列{an}中，a1=8,a4=2且满足an+2=2an+1－an,（n∈N*）。
（1）求数列{an}的通项公式；
（2）设Sn=｜a1｜+｜a2｜+…+｜an｜,求Sn。
正确答案
解：（1）由an+2=2an+1－an
d=
（2）由an=10－2n≥0可得n≤5，当n≤5时，Sn=－n2+9n，当n＞5时，Sn=n2－9n+40，故Sn=
解析
解析已在路上飞奔，马上就到！
知识点
19.设数列
（1）设
（2）求数列
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
22.已知
（1）求
（2）若对一切
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21.已知平面向量a=（
（1）证明a⊥b；
（2）若存在不同时为零的实数k和t,使x=a+ （t2–3）b，y=–ka+tb，且x⊥y,试求函数关系式k=f（t）;
（3）据（2）的结论,讨论关于t的方程f（t）–k=0的解的情况。
正确答案
（1）证明：∵a·b=
（2）解：∵x⊥y,∴x·y=0
即［a+（t2–3）b］·（–ka+tb）=0，整理后得
–ka2+［t–k（t2–3）］a·b+t（t2–3）·b2=0
∵a·b=0,a2=4,b2=1
∴上式化为–4k+t（t2–3）=0，∴k=
（3）解：讨论方程
于是f′（t）=
令f′（t）=0,解得t1=–1,t2=1.当t变化时，f′（t）,f（t）的变化情况如下表：
当t=–1时，f（t）有极大值，f（t）极大值=
当t=1时，f（t）有极小值，f（t）极小值=–
而f（t）=
所以f（t）的图象大致如下：
于是当k>
当k=
解析
解析已在路上飞奔，马上就到！