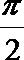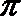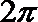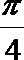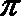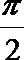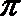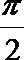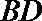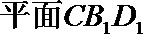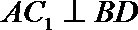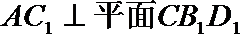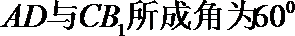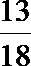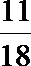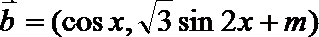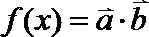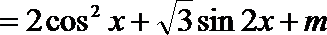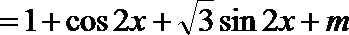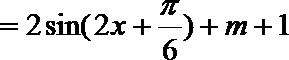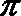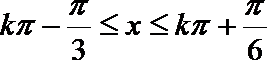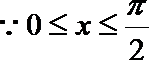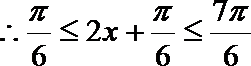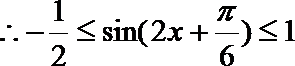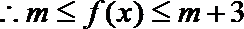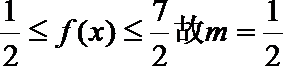- 真题试卷
- 模拟试卷
- 预测试卷
1．若角
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．设点P是函数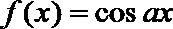
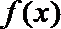
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．设函数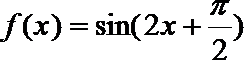
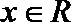
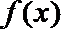
A最小正周期为
B最小正周期为
C最小正周期为
D最小正周期为
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．函数
的部分图象如图，则（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．
A
B
C
D异面直线
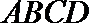
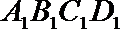
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
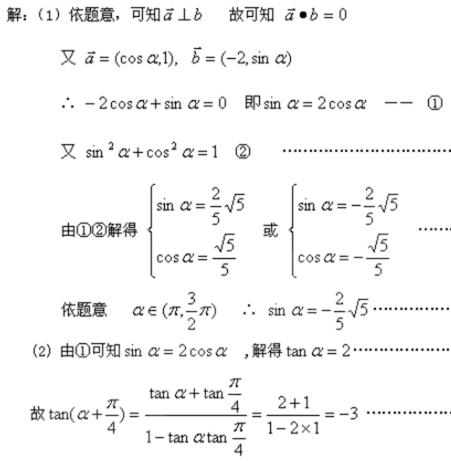
8．已知向量
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．设两个平面
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．已知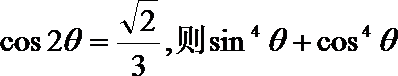
A
B
C
D－1
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．半圆的直径AB＝4, O为圆心，C是半圆上不同于A、B的任意一点，若P为半径OC上的动点，则
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知数列{
A
B
C2
D3
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．关于函数
① 
② 
③ 
④ 
⑤ 若
⑥ 
其中正确命题的序号有（ ）
正确答案
①④
解析
解析已在路上飞奔，马上就到！
知识点
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．已知
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．三棱锥A－BCD中，BA
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．如图所示，四边形ABCD是矩形，
（1）求证：AE
（2）求证：AE//平面BFD；
（3）求三棱锥C-BGF的体积。
正确答案
（1）∵ 
∴ 
∵ BF
又
∴ AE
（2） 依题意，易知G为AC的中点
又∵ BF
∴ 可知F为CE的中点
故可知 GF//AE
又可知
∴ AE//平面BFD
（3）由（1）可知AE
∴ GF
又 
∴
∴ 三棱锥C-BGF的体积为
解析
解析已在路上飞奔，马上就到！
知识点
20．设函数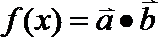
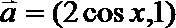
（1）求函数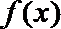
（2）当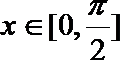
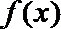
正确答案
（1）∵
∴函数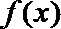
可知当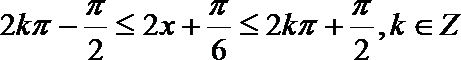
解得
故函数单调递增区间为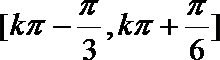 
（2）
又
解析
解析已在路上飞奔，马上就到！
知识点
17．已知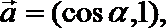
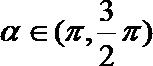
（1）求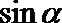
（2）求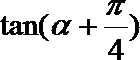
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．数列{
（1）求
（2）求{
正确答案
（1）依题意 
∴ 
∵ 
即 
又C是不为零的常数，所以
（2）由（1）知
∴ 当
将以上各式累加得
∴
检验得
解析
解析已在路上飞奔，马上就到！
知识点
21．如图,在四棱锥P-ABCD中,底面ABCD为菱形, 
（1）若PA=PD,求证: 平面PQB
（2）点M在线段PC上，PM＝
正确答案
（1）依题意，可设
由余弦定理可知
∴
故可知 
(另解:连结BD,由
又在
∴
∴
又
（2）连结AC交BQ于点O ，连结MO，
欲使 PA//平面MQB
只需 满足 PA//OM 即可
又由已知 AQ//BC
易证得 
故只需 
∵
∴可知 PA//OM 又
所以可知当 
解析
解析已在路上飞奔，马上就到！
知识点
22.已知函数
（1）若
（2）在（1）的条件下，若关于x的方程
（3）若存在
正确答案
（1）
由题意得
（2）由（1）知
令
当x变化时，
∵关于x的方程
（3）由题意得，
①若
∴当
②当a>0时
由
综上得a>3.
解析
解析已在路上飞奔，马上就到！